← Introduction. | Historical Context
Counting, numbers and counting technologies - did one come first?
Any account of the history of mathematics is to an extent thwarted by the fact that mathematical capacity, and almost certainly mathematical thinking, extends back beyond the time of recorded human history. There is by now growing evidence that some mathematical capacity is shared not only by humans but also by a range of animals, including monkeys and some fish and birds.1 In short, some of our mathematical reasoning probably reflects an evolved endowment of the human brain. For that reason, the axiom that equals subtracted from equals leaves equals (one of Euklid’s “common opinions”), is perhaps something we “know” rather than “arrive at”.
Nevertheless, while clearly there are capabilities in the human brain which enable the assessment of quantity, we need to resist the temptation to believe that particular mathematical capacities are ‘hard wired’ through evolution (and then make some retrospective argument about how that would have been good for survival). Some underlying capacities no doubt are, but determining what of them are is a difficult process. Indeed, supported by a range of new highly revealing imaging technology there is increasing recognition within the field of neurophysiology that brains, including the human brain, are remarkably “plastic” in their capacity to reorganise themselves in relation to context. Thus the brain itself may be “rewired” to increase its capacity to reason mathematically depending on how we, and that sense we as members of a culture, think. This in turn is shaped in part by the way we shape our context, and not the least by the technologies we create to assist us. Thus for example, in the first half of the last century there was increasing social demand to be able to do mental arithmetic. So quite possibly we developed within our brains enhanced capacities to do that. With the advent of personal computing machines that capacity is less called upon. As has been pointed out forcefully more generally about computers and the internet,2 from this point of view, calculators, as we create and use them, may be reshaping our brains and their capacities to do certain forms of mathematical and associated reasoning.
It may be useful to think of the emergence of counting in an unusual way (at least in terms of the literature). First we may recall that in the approach to ‘artificial intelligence’ in which networks are set up using computers to mimic the neurological networks in the brain, these prove remarkably effective in pattern recognition.3 The distinction between counting and pattern recognition can be fine indeed in experiments carried out with animals (for instance chicks who when imprinted with five objects as constituting their ‘mother’ then search for her when two of the objects are removed)4 Similarly, recently it was reported that a neural network which had not be programmed with the concept of number was able to develop a capacity to identify patterns which had more dots.5 Said the leader of the research, Marco Zorzi (University of Padua) “It answers the question of how numerosity emerges without teaching anything about numbers in the first place.”6
Another clue to the long-standing nature of the required evolutionary endowments is found with experiments with baboons which were able to be taught not only to discriminate between four letter English words and nonsense combinations but also to achieve increased capacity to guess whether a word they had not seen before was an English word.7 This shows the surprisingly sophisticated and relevant capacities of pattern recognition likely to have been possessed even by the human species’ evolutionary ancestors.
It is possible therefore that the act of counting is one where an evolutionarily endowed physical capacity for pattern recognition is complemented by the capacity to manipulate objects (whether fingers, marks on bones, or counters) thus constructing abstract formulations of the pattern in relation to observed patterns. From this the invention of words to associate with the abstraction is but one additional step, and symbols as shorthand for those words, another. This raises the interesting question of whether the usual assumption that calculators were invented to assist counting should be reversed, with the possibility that the (very rudimentary) calculator was a necessary step towards developing counting.
One technological practice which is believed to have existed as long ago as the Upper Paleolithic period (40,000–10,000 years ago) in the region of Lower Austria (Moravia) and South Poland, is weaving. In excavations (dated as early as 35 thousand years ago) imprints of textiles have been found on the surface of some ceramic fragments. 8 Weaving certainly involves a capacity for pattern recognition, and perhaps some concept of tracking the quantity of successive threads. Perhaps then, this is an early indication of the building blocks for mathematical thinking already in play.
There is by now evidence from both anthropological and psychological research relating both to the oral presence of numbers in different societies and the presence of written words or symbols for them. Indeed this has led to the emerging field of ethnomathematics. However, the conclusions are not clear cut. It may be as simple as whilst we all share some basic capacity to do counting and mathematical thinking, what that is is hard to pin down, and in any case, whether and how that capacity is taken up and developed depends on the cultural and historical circumstances and needs of a culture. Indeed, whilst there are differences in what we recognise as mathematical cognitive abilities in different societies it seems that these differences cannot be taken to “imply necessary distinctions between right/wrong, simple/complex or primitive/evolved.”9
There is plenty of archeological evidence that the capacity to count is very ancient. Boyer and Merzbach suggest that it came about first through recognition of sameness and difference, and then over time the recognition that collections of things with sameness can be given a short description which we now call number. They suggest this process was probably very gradual and may have evolved very early in human development, perhaps some 300,000 years ago about the same time as the first known use of fire.10. However they are also quick to note that whilst we may make conjectures about the origins of the concept of counting, since counting emerged prior to the earliest civilisations and certainly before written records, “to categorically identify a specific origin in space or time, is to mistake conjecture for history.”11
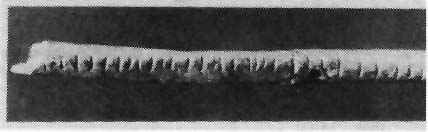
Nevertheless, there is evidence that the idea of associating things to be counted with a set of abstract counters is long standing. A Baboon bone dated from 35,000 years ago (amongst others of similarly great age) has been found with what are believed to be tally marks scribed on it.12 Another more recent bone, from about 11,000 years ago found in the village of Ishango at one of the farthest reaches of the Nile, has a much more complex set of notches which may be calculating tables, but is probably a crude lunar calendar.13
Small piece of fibula of a Baboon marked with 29 well defined notches ~35,000 BCE14
The prevalence of five and ten based counting systems in the most ancient surviving records suggests that the fingers also have long been used as a handy, although not universal, set of counters. (The Kewa people of Papua New Guinea are reported to count from 1 to 68 on different parts of their bodies.)15 The earliest counting, it has been suggested, may likely have been with pebbles, which were both convenient but whose use in this way may prove illusive to discovery through contemporary archeology.16
There may be a temptation to suggest that the earliest surviving instance or record of a calculator constitutes the moment of the emergence of the technology of calculation, but as the above suggests, this is a crass simplification. Even beyond fingers and stones the earliest approaches may have been made of fragile organic materials, which except perhaps in very dry graves, would be unlikely to stay the distance. Thus for example we do not know how early devices such as the knotted string khipu of the Incas was used. We do know that this device, always composed of many strands of knotted strings, but with great diversity in its use, not only represented a decimal, double entry accounting system, but also was used in functions of state, from recording outcomes of the national census as carried out district by district, and then compiled nationally, to the calculation of tributes, culturally significant astronomical events, and much more.17
Khipu of 322 strands said to be from Nosca, Peru18
The earliest objects recognised by archaeologists as surviving tokens for counting and (primitive) accounting can be found from 8,000 BCE in the remains of Neolithic settlements, at a time of early deployment of agricultural practices, in what is now Syria and Iran. Success in agriculture could be enhanced by record keeping as well as exchange since settlement enabled an increasingly sophisticated division of labour to emerge. Over the next five thousand years (to 3,100 BCE) these artifacts can be seen to evolve to tokens (essentially pebbles fashioned from clay but with different shapes to connote different things, such as a cylinder representing one animal, or a cone representing a quantity of grain).
Set of complex tokens from Susa, Iran, from ~3350–3100 BCE19
These tokens were in time enclosed in clay envelopes holding tokens of particular transactions strung together on strings. Envelopes, however, hid the enclosed tokens and so envelopes emerged bearing images of the contained tokens impressed on their surfaces, and beyond that to clay envelopes with signs not merely impressed upon them but also scribed into them.

Envelope and tokens from Susa, Iran, 3200–3100 BCE20
As Schmandt-Besserat points out in her important, although not uncontested account,21 “The substitution of signs for tokens was no less than the invention of writing.” 22 This supports the observation, made by several authors,23 but developed in considerable detail by Schmandt-Besserat that these inscriptions not only preceded the appearance of the first known written alphabet (Cuneiform) but also appear to prefigure it. This lays a basis for the intriguing proposition that rather than writing being the basis for mathematics, the primitive technologies of calculating (and the mathematics that underlies it) may have not only preceded but formed the basis for the development of the first written scripts which lie at the heart of the emergence of the technology of writing.
The Sumerian civilisation as already mentioned was the source of cuneiform script, the earliest known alphabetic writing system. With an advanced system of settlements, agriculture, irrigation and social organisation it flourished in the fertile plain of Mesopotamia between the Tigris and Euphrates rivers, in the period prior to 3,500 BCE. The number system developed within the cuneiform script was based on powers of sixty rather than powers of ten as in contemporary systems, although these ‘sexagesimal’ numbers were in point of fact constructed with patterns corresponding to the numbers from 1 to 10. During the period of Akkadian rule, which lasted to 2100 BCE, the abacus entered Sumerian life creating a further extension to the capacity to form basic arithmetic operations. The Babylonian civilisation replaced that of the Sumerians around 2000 BCE.
Large numbers of cuneiform tablets found in archaeological digs reveal that by now a mathematical system, recognisable to modern sensibilities, had emerged. This went hand in hand with the development of an organised urbanised agricultural society with significant construction work (especially of canals). The day was divided into 24 hours, the hour into 60 minutes, the minutes into 60 seconds, and the circle was divided into 360 degrees, in all of which the sexagessimal flavour persists to the present. The tablets showed now the construction of reference tables to aid calculation including squares of numbers, tables of reciprocals to aid division, and more.

Babylonian scribal school tablet showing list of reciprocals ~1700 BCE24
A basic form of algebra had also been developed, with equations and solutions, including solutions to quadratic equations that arose in the course of their engineering of canals and other structures.25 Schools were also constructed so that the knowledge required to read and write cuneiform, and perform mathematical operations using it, could be transmitted.26 In this sense, now recognisably analogous to modern writing and media, the cuneiform tablets, combined with a social order which both needed it, and trained in its use, more than 3,000 years ago had emerged as a socially powerful mathematical and scribal technology.
The idea of numerals to represent numbers diffused and developed over following centuries emerging in different representations in different places. True to the importance of the human hand, most of these systems privileged the number 5 and 10, with 10 emerging as the most common “base” the powers of which shaped the meaning of successive positions in a string of numerals. Two different innovations should be distinguished here. The first is to develop numerals corresponding with successive quantities. The second is to develop a “place value” system of writing them where the place that they occupy represents, as it does in modern numbers, the number written multiplied by a power of the base. (That is in modern script, 123 represents 1 multiplied by 10×10 + 2 multiplied by 10 + 1 multiplied by 1).
It is unwise to assume that the history of counting, numbers, and indeed script has a single line of development. For example, Stephen Chrisomalis cautions us, it is highly probable that “the modern place value numerical notation, or something quite like it, developed at least five times idependently” - in: Mesopotania (as already mentioned ~2100 BCE), China in ~14–1300 BCE, India in ~500 CE, and the Andes in or before 1300 CE, with the explanation that it is not as big a cognitive leap to develop such a system when it proves useful as is often suggested,27 (or to put it another way, some combination of our biologically endowed cognitive capacities and underlying evolved cultural building blocks may be conducive to assembling quantities in this way).
Some 100 different scripts have been identified which have emerged over the last five millennia.28 Of these numeric scripts, however, the earliest dated are the Proto-Cuniform (already discussed) and the Ancient Egyptian. The Ancient Egyptians developed a number system which was different in the base (this time 10 rather than 60 in cuneiform) and in the characters used. The ancient Egyptian system of hieroglyphic numerals, developed as early as 3250 BCE,29 had characters for 1 and then the powers of 10 (10 - a vertical stroke, 100 - an inverted wicket, 1000 a snare, etc.) with the numbers from 1 to 9 simply shown as the corresponding repetition of the number 1. Thus for example, the number 12345 would appear as 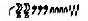 .30 However, after about a millennium of use of this system another “Hieratic” script was developed for use on Papyrus for routine use as opposed to the hieroglyphic script which was retained for carving in rock. The Hieratic numerals (shown in the table below) had by now taken what to modern eyes is the more efficient form of single symbol “ciphers” to represent each of the integers from 1 to 10, the same concept which forms the basis for the modern numerals in use today.
.30 However, after about a millennium of use of this system another “Hieratic” script was developed for use on Papyrus for routine use as opposed to the hieroglyphic script which was retained for carving in rock. The Hieratic numerals (shown in the table below) had by now taken what to modern eyes is the more efficient form of single symbol “ciphers” to represent each of the integers from 1 to 10, the same concept which forms the basis for the modern numerals in use today.
As shown in the table below, other early representations similarly drew directly on patterns representing counters (or fingers - even the Roman system can be seen as counting to five on the one hand, reserving the thumb and forefinger for the V to represent five, and the X representing a V on each hand). The Egyptian Hieratic and then the Greek system replaced combination numerals with single characters, and finally, from the eight century, the familiar symbols of the modern (arabic-Indian) place-based system (complete with the numeral 0 to replace earlier spaces for “place holders” finally emerged.31
| Number System | Script32 | Base | ~ Century Introduced33 |
| Proto-Cuneiform |  | 60 | 3200 BCE |
| Egyptian Hieroglyphic34 |  | 10 | 3200 BCE |
| Egyptian Hieratic35 | 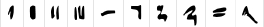 | 10 | 2600 BCE |
| Greek | 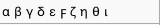 | 10 | 575 BCE |
| Roman |  | 10 | 500 BCE |
| Chinese Rod |  | 10 | 300 BCE |
| Indian36 C8 CE | 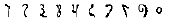 | 10 | 700 CE |
| Arabic37 C11 CE | 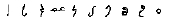 | 10 | 1000 CE |
| European38 (Arabic-Indian) C15 CE | 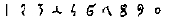 | 10 | 1400 CE |
| Modern (Arabic-Indian) C16 CE | 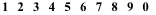 | 10 | 1549 CE39 |
← Introduction. | Historical Context
1 see for example, papers cited in Michael Tennesen, “More Animals Seem to Have Some Ability to Count”, Scientific American, September 2009, viewed 19 Dec 2011 (↑)
2 Nicholas Carr, The Shallows: What the Internet is Doing to Our Brains, W. W. Norton, New York and London, 2010 (↑)
3 Brian D. Ripley, Pattern recognition and neural networks, Cambridge University Press, UK, 1996 (↑)
4 Tennesen, Scientific American, op. cit. (↑)
5 Ivilin Stoianov and Marco Zorzi, “Emergence of a ‘visual number sense’ in hierarchical generative models”, Nature Neuroscience, advance online publication, Sunday, 8 January 2012/online, http://dx.doi.org/10.1038/nn.2996 (viewed 21 Jan 2012) (↑)
6 Celeste Biever, “Neural network gets an idea of number without counting”, New Scientist, Issue 2848, 20 Jan 2012. (↑)
7 Jonathan Grainger, Stéphane Dufau, Marie Montant, Johannes C. Ziegler, Joël Fagot, “Orthographic Processing in Baboons (Papio papio)”, Science, Vol. 336 no. 6078, 13 April 2012, pp. 245–248. (↑)
8 J.M. Adovasio, O. Soffer, D.C. Hyland Textiles and cordage, Pavlov I – Southeast: A window into the Gravettian lifestyles, Dol. Vest. Stud. 14, Brno, 2005, p. 432–443, cited in Jiří A. Svoboda , “The Gravettian on the Middle Danube” Paléo [En ligne] , 19, 2007 , mis en ligne le 23 avril 2009, Consulté le 21 décembre 2011 (↑)
9 Stephen Chrisomalis, “The cognitive and cultural foundations of numbers”, Oxford Handbook, pp. 495–502. (↑)
10 Carl B. Boyer and Uta C. Merzbach, History of Mathematics, Wiley, 2010, p. 2. (↑)
11 ibid p. 7. (↑)
12 ibid p. 3. (↑)
13 D. Huylebrouck, “The Bone that Began the Space Odyssey”, The Mathematical Intelligencer, Vol. 18, No. 4, pp. 56–60 (↑)
14 Jonas Bogoshi, Kevin Naidoo, John Webb, The Oldest Mathematical Artefact, The Mathematical Gazette, Vol. 71, No. 458 (Dec., 1987), p. 294. (↑)
15 Frank J. Swetz, “Bodily Mathematics” in From Five Fingers to Infinity: A Journey through the History of Mathematics, Open Court, Chicago, 1994, p. 52. (↑)
16 Denise Schmandt-Besserat, “The Origins of Writing: An Archaeologist’s Perspective”, Written Communication, Vol 3, 1986, p. 35. (↑)
17 Gary Urton, “Mathematics and Authority: a case study in Old and New World Accounting”, in Robson and Stedall, The Oxford handbook, p. 34–49. (↑)
18 From the Museum for World Culture, Göteborg, Sweden. Image retained in the Harvard University Khipu Database http://khipukamayuq.fas.harvard.edu/images/KhipuGallery/MiscAlbum/images/UR113%20Valhalla_jpg.jpg (viewed 27 Dec 2011) (↑)
19 Denise Schmandt-Besserat, “The Origins of Writing : An Archaeologist’s Perspective”, Written Communication Vol 3, No1, January, 1986, Figure 3, p. 41. (↑)
20 Denise Schmandt-Besserat, “The Envelopes That Bear the First Writing”, Technology and Culture, Vol. 21, No. 3, July 1980, Figure 1, p. 358. (↑)
21 see for example, Zimansky, “Review of Schmandt-Besserat 1992”, in Journal of Field Archaeology, Vol. 20, 1993, pp. 513–7. (↑)
22 Schmandt-Besserat, Written Communication, 1986, p. 37. (↑)
23 for example, Livio C. Stecchini, “The Origin of the Alphabet”, American Behavioral Scientist, Vol 4, February, 1961, pp. 3–7 (↑)
24 Eleanor Robson, “Mathematical Education in an Old Babylonian Scribal School”, in Robson and Stedall, The Oxford handbook, Figure 3.1.4, p. 210. (↑)
25 ibid (↑)
26 Eleanor Robson, “Mathematics education in an Old Babylonian scribal school”, in Robson and Stedall, The Oxford handbook, pp. 209–227 (↑)
27 Chrisomalis, Oxford Handbook, p. 509. (↑)
28 Stephen Chrisomalis, “A Cognitive Typology for Numerical Notation”, Cambridge Archaeological Journal Vol 14, Issue 1, 2004, p. 37. (↑)
29 ibid, p. 51. (↑)
30 characters reproduced from Boyer and Merzbach, History of Mathematics, p. 10 (↑)
31 For a more detailed account of the multiple scripts which emerged and a classification of them see Georges Ifrah, The Universal History of Computing: From the Abacus to the Quantum Computer, John Wiley & Sons, USA, 2001, pp. 26–63. (↑)
32 except where otherwise indicated script images reproduced from Wikipedia (viewed 23 Dec 2011) (↑)
33 Chrisomalis, Cambridge Archaeological Journal, 2004, pp. 51–2. (↑)
34 image created with MS Word (↑)
35 script images reproduced in modified form from David Kerkhoff, “Hieratic Numerals” http://www.dafont.com/hieratic-numerals.font (viewed 24 Dec 2011 (↑)
36 script images reproduced in modified form from Jan Meyer, “Die Entwicklung der Zahlensysteme” http://www.rechenhilfsmittel.de/zahlen.htm (viewed 17 Jan 2012) (↑)
37 script images reproduced in modified form from Jan Meyer, ibid. (↑)
38 script images reproduced in modified form from Jan Meyer, ibid. (↑)
39 An accurate rendition of Modern numerals appears on the title page of Juan de Yciar, Libro Intitulado Arithmetica Practica, Zaragoza, 1549 (↑)
Pages linked to this page
 This work by Jim Falk is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License Click on the logo to the left to see the terms on which you can use it.
This work by Jim Falk is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License Click on the logo to the left to see the terms on which you can use it.