« Part 1 Origins | | Part 3 The Late Modern Period (1800-) »
Part 2. The Modern Era
| Mini: PHP-GD image library not found. Exiting. | Mini: PHP-GD image library not found. Exiting. | Mini: PHP-GD image library not found. Exiting. | Mini: PHP-GD image library not found. Exiting. | Mini: PHP-GD image library not found. Exiting. | Mini: PHP-GD image library not found. Exiting. |
On this page… (hide)
The “Modern Era” (or the “Modern Epoch”) is taken as stretching from the mid-sixteenth to mid-twentieth centuries.1 This was a period of accelerating change in Europe and, amongst much else, a new burst of innovation in mathematics and mechanical calculating technology.
Even by the late sixteenth century in practice methods of calculation had not changed much since the Roman Empire. Indicative of this “calculi” (Latin: “calculus” for “pebble” (or “limestone”) - the origin of the word “calculation”) were still being struck (as they had been for centuries) to facilitate counting and arithmetic especially in many fields of commerce. They were referred to differently in different places. One such - a French “jeton” from 1480–1520 is shown below. It is made to look like a coin, but its inscription is meaningless.

Sides 1 & 2, French jeton 1480–1520
(collection Calculant)
Sometimes these calculi (however named, and in whatever form they took) would be “cast” on a “counting board”. Sometimes they would be simply piled up to aid the process of accounting or calculation. Their use petered out in England over the C18 and similarly in France ending with the revolution (1789).2 There was in particular a contest between the incoming technology of pen and paper using arabic numerals, and calculi and counting board based on Roman numerals. This contest is shown in the following woodcut from 1503,3 where, presided over by Dame Arithmetic, on the left Pythagoras is using the new technology, whilst on the right the ancient Roman mathematician Boethius is calculating with counting board and calculi.

Contested methods - Woodcut from 1503
For such counting boards the horizontal lines represent rows of multiples of 1, 10, 100, 1000 (or in Roman numerals I, X, C, M), whilst the mid point between those lines represent the half-way mark of 5 (V), 15 (XV), 50 (L), 500 (D) and 1500 (MD). For addition the number on the left could be progressively added to the number on the right by rows. In the woodcut, Boethius is adding the number MCCXXXXI (1,241) on his left (our right), to the number LXXXII (82) on his right. (Multiplication could be done by repeated additions.4)
As the use of calculi reached its zenith they became important in other ways. The example minted in the Netherlands in 1577 shown below (Calculi) demonstrates that by then, counters were in such general use that they were being used to convey messages to the public - becoming the equivalent of official illustrated pamphlets.5 The face on the left (“CONCORDIA. 1577. CVM PIETATE”) translates (loosely) to “Agreement. 1577. With Piety” and seems to carry the visual message that we are joined together (with hearts and hands) under our ruler (the crown) and God (represented by a host). The opposite face (“CALCVLI.ORDINVM.BELGII. Port Salu”) shown on the right) translates to “Calculi. The United Provinces of the Netherlands, Port Salu” and shows a ship (perhaps the ship of state)6 coming into Port. (The term “port salu” at the time often simply meant “safe harbour”). It was not a calm time. It was in the midst of the European wars of religion (~1524–1648), and in particular the Eighty Years’ War in the Low Countries (1568–1648). It was only 28 years after Holy Roman Emperor Charles V had proclaimed the Pragmatic Sanction of 1549 which established “the Seventeen Provinces” as a separate entity. (This comprised what with minor exception is now the Netherlands, Belgium and Luxembourg.) Given that there had been a revolt in 1569 (leading to the Southern provinces becoming subject to Spain in 1579), only two years after this calculi was minted, we may presume that the messages of widespread agreement, safe harbour and rule from God might have been intended as a calming political message.

| 
|
| CONCORDIA.1577.CVM.PIETATE. | CALCVLI.ORDINVM.BELGII. PORT SALV |
| 1577: Sides 1 & 2 of calculi | (collection Calculant) |
The system of “pebble” or “ocular arithmetic” using counters stretched back seemingly into the mists of pre-history. But in the middle of the sixteenth century a process of dramatic change was beginning. It heralded the re-growth of political power in Europe and Britain. Over the next two centuries this would be accompanied by a dynamic development in knowledge, trade and innovation. By the beginning of the eighteenth century the industrial revolution in the “West” would be well underway. Drawing from earlier innovation in the “East” this now outpaced it in terms of economic and political power and technological innovation. It was a time of increasing fascination with new knowledge and mechanisation, continuing rise in scale and economic importance of cities, growth of what became industrial capitalism. Increasing dominance of institutions of the market (including the modern corporation) shaped also new products produced by increasingly sophisticated technological means. In support of this, availability of paper and literacy spread. Roman numerals were increasingly replaced by their Arab-Indian counterparts in every-day use, and the reliance on “ocular arithmetic” with counters was on the decline. Developments in mathematics and calculation, although important, were just one component of this remarkable transition.
1. Change and the Modern Era
Central to this period of change was the extent to which the feudal system of organisation, that had dominated life in Europe and Britain for more than a millennium, was now being undermined. From the thirteenth to sixteenth century improvement in agricultural practices (for example, the introduction of the three-field system and improvements in ploughing) had allowed much more food to be produced from the same land. With less labour devoted to agriculture there had been more available for diversification into production and trade in an increasing variety of commodities. This marked the first phase of the transition from feudalism to an increasingly dominant capitalist economic and political system.
The feudal system of land had been controlled through a system of manors by feudal secular and religious lords (and more elevated nobles). Church and state supported a view of the feudal order as natural and immutable - one in which lords and serfs performed enduring roles within a system of mutual obligation. As agriculture became more efficient increasing numbers of “free men” with greater social mobility began to challenge the entrenched ways and power of the feudal system. Freed from the obligation of labouring on the land, as early as the eleventh and twelfth centuries, these freemen began to find new work as merchants or in other productive occupations first in towns, and then large industrial towns. Unshackled also from the manorial system their allegiance was more directly to kings (queens and princes) rather than lords. As merchants became more numerous they increasingly gained the concessions from the Royal courts necessary to carry out ever more sophisticated forms of commerce.7
The effect of the burgeoning new economic transactions, supported by new rights and laws, was to increase both the power of merchants and the royal courts (initially at least) in comparison to that exercised by the feudal lords. Ownership of the means of production (land, buildings and technology) was passing to the hands of a new economic class. The richer owners of land bought up the land of others enabling them to apply improvements such as the use of fertilisers and specialisation in crops and animals. At the same time the factory system was emerging, first as a form of control, then as a place for deploying new technologies of production. At first, merchants moved from simply selling the product of the peasants’ labour, to organising its production and selling it. For example, in the case of woollen cloth, rich merchants began to “put out” orders to peasants for the wool. Peasant weavers and sewers were gathered into employment in factories where cloth would be made, or fashioned into clothing. Richer merchants began to commission the application of new technologies in their factories, to cheapen and speed production.
By the late eighteenth century and into the nineteenth new technologies were shaping commerce. These included the telegraph, steam power, the railway, and the development of the factory system now powered with such technologies. The feudal system became increasingly submerged by the ever more dynamic, productive and powerful force of the industrial revolution.8 Trade was increasing not only in volume but also reach. New technologies of navigation and shipping were resonating with new means of production, forms of transportation, and ways of transmitting information. Whilst in 1750 it had taken as long to travel or send information from one place to another as in the ancient Greek or Roman empires, by the end of the following century travel by railway across great distances was becoming vastly faster, and information could be sent by telegraph nearly instantaneously. Factories, trade and cities all expanded as the needs of the new system were met and fed. The celebration of technology, and use of it for all aspects of this transition to industrial production, was becoming a central tenet of Modern life.
2. Strands of change
This turbulent time was both a fertile ground for the development of new knowledge (including mathematics), and the application of that knowledge to the practical work of production (including technologies of calculation). However, diverse developments were occurring, across different parts of the societies. Perhaps confusingly all of these strands were to some extent intertwined. Some of the more important of them are discussed below.
2.1 Aristocrats, artisans and the rekindling of critical inquiry
Key to the spirit of change that was taking place was a renewed fascination with learning and innovation. The certainties that had supported the established feudal order were, from the fourteenth century and over the next three centuries, increasingly challenged. The approaches which eventually became known as “science” (in its Modern sense) were beginning to be promoted and gain support. What began to be proposed and then taken up was a systematic and incremental process of discovery based on the practical investigation of empirically testable hypotheses built on the basis of prior work, the whole being subject to critical peer response.
It has been estimated that in 1668 in England “the temporal and spiritual lords, baronets, knights, esquires, gentlemen, and persons in offices, sciences, and liberal arts” together represented about 4% of the population9, (although enjoying about 23% of the income).10 Clearly those associated with the sciences in general, and mathematical work in particular, constituted only a tiny fraction of this. It may have been an initially small group of people involved, but as inevitably it was drawn from those who could afford the ‘time out’ to devote themselves in this work, drawn as they often were from aristocratic families, they had the capacity to convey their excitement at new insights amongst those of standing, and not least to reach the ears of royalty.
The role of the emerging practice of science became particularly confrontational for religious authorities (and particularly the powerful Catholic Church). Astronomical observation and theory had long played an important role in human life. Apart from its traditional role in astrological prognostication, astronomy could be turned to the prediction of seasonal changes such as tides, and the fixing of time and position. However, religious orthodoxy was the Ptolemaic concept that the Earth lay at the centre of the universe with the planets, sun and stars revolving around it in concentric spheres. The seminal work of Nicolaus Copernicus De revolutionibus orbium coelestium (On the Revolutions of the Heavenly Spheres) was published in 1543 (just before his death) providing a systematic justification of a view of the solar system in which the planets, including the Earth, revolved around the sun. This sparked a major theological and scientific controversy. Whilst Copernicus had the planets moving in circles, it remained for the German mathematician, astrologer and astronomer, Johannes Kepler, in 1609, to publish mathematical arguments showing (amongst other important insights) that a much simpler explanation was that the planets move in ellipses.11 Steadily the convergence of observation and mathematical insight was bringing astronomy from an adjunct to philosophical speculation and theological dogma, to a science of the motion of the heavenly bodies. It was not however, until 1758, that the Catholic Pope of the time removed Copernicus’s book from the index of forbidden reading.
The desire to predict the motion of heavenly bodies in itself provided demand for not only more powerful mathematical insights, but also aids to calculation. Astronomical investigation was based on observations of planets and stars where the calculated paths were redicted from a theory which involved not circular cycles, but also epicycles and ellipses. Making such predictions required a vast number of calculations involving repetitive additions and multiplications. New ways would soon be developed which could help with this.
In addition, despite theological concern associated with the rekindling of scientific interest, “the idea of progress” was finding particular favour with the increasingly powerful merchant class. An underlying promise here was that, rather than awaiting one’s rewards for the afterlife, technical and industrial development could increasingly be relied on to satisfy needs in the here and now.12 “The idea of progress” stressed a claimed progressive character to science. Over time, seized on by the emerging entrepreneurial class it came to be part of an argument for the new order, built around the market, to be given greater freedom to act, and corresponding political standing. As a consequence, as Bury puts it, during this period increasingly “Self-confidence was restored to human reason, and life on this planet was recognised as possessing a value independent of any hopes or fears connected with a life beyond the grave.”13
The idea of progress was an ideology which could give legitimacy to the claims of a particular emerging class. But it was based on developments in thinking that were led by a comparatively small set of intellectuals. The questions they worked on often would have seemed quite divorced from everyday life. These mathematical and other scientific pioneers were frequently drawn from the aristocracy or church, or at least were gentlemen of considerable independent means. The motivations for doing this work might be scattered across a spectrum. It could include: a delight in learning and discovery, a desire to build prestige amongst peers, a hope for economic return from practical applications, or a desire to find favour with a rich or royal patron. Over time an increasing number of kings, queens, and other nobles began to enjoy being seen as a supporter of progress, or became interested in the work of intellectual pioneers.
A gulf still stood between the discoveries by mathematicians and other intellectuals, and the many others to whom this work could be of practical assistance. On the one side of that gulf, reflecting upon these early intellectual innovators, was the long-standing idea that a man of elevated (or aristocratic) heritage - a “gentleman” or in France “un honnête homme” - would consider it demeaning (as would an ancient Greek or Roman of standing some 1500 years before) to lower himself to associate himself with practical work. On the other side, amongst those whose life was devoted to practical work (for example, artisans) a parallel image was common, of the impractical nature of the gentleman mathematician and the products of mathematical thinking. This gulf would have to be surmounted before these the technical insights of these “gentlemen” could be turned to widespread practical purpose.
The beginnings of the renewal of mathematical and scientific learning thus did not amount to a neat picture. Old ways of doing things lay not just with the aristocracy. As Spencer Jones points out,14 even into the seventeenth century whilst learned men began to press forward mathematics, navigation remained “a practical art, in which successes depended upon experience, common sense and good seamanship. The navigator had for his use the compass, the log, and some sort of cross staff” with which, together with his estimate of wind speed and currents, he would estimate his position by a “crude method of dead reckoning”.
Mathematics was not taught in schools, and where it was pursued, as with the rest of science, it tended to be the pursuit of those with sufficient (often inherited, or previously accumulated) resources to do so. Thus, as one writer, in 1701, put it:
Nevertheless, over time, the usefulness of technical developments, including the outcomes of mathematical calculation in astronomy, engineering, and commerce would break through the barriers of traditional practice. And despite the reticence still evident in 1701, the pressure to compete effectively in trade and warfare would increasingly lead to deliberate efforts to utilise the outcomes of the work of the “Speculative, Retir’d, Studious Men”.
2.2 Trade, navigation and shipping and the developing economy.
Even prior to the Modern era, the increasing importance of mercantile and thus also naval shipping was reshaping the understanding of needs especially at the level of government. Early developments around navigation and the construction of ships enabled more reliable open sea transport and naval expeditions. By the mid fifteenth century Portuguese ships had rounded the Cape Bojadar on the West Coast of Africa (in 1434), and the quadrant and a few decades later the astrolabe (in about 1480) had come into use.16
The second half of the fifteenth century through the sixteenth century was a time of such dramatic European exploration by sea that it is often referred to as “the age of exploration”. Notable amongst the European achievements were the charting of sea routes to India, Africa and the Americas. (Christopher Columbus reached America in 1492, whilst Sir Francis Drake claimed San Francisco Bay for Queen Elizabeth in 1579.) As a consequence, there was a large flow of gold and silver, amongst many other commodities, from the Americas to Europe. This was the source of a powerful inrush of wealth and thus investment and purchasing power for those who gained possession of it.17 Increasingly complex financial techniques were needed to take advantage of long-distance trade.18 This was but an early contribution to the increasingly complex financial flows, instruments and organisations which would be developed in support of, and in order to gain advantage, in the increasingly complex market capitalist economy. This economy would develop over the next several centuries creating ever greater demands for an ever more distributed capacity for efficient calculation.
Innovation requires multiple inventions. Once they are applied in practice this creates new opportunities for innovation creating a dynamic system of change. Increased navigation meant increased trade, requiring increased naval protection of trading routes, requiring improved navigation. The improvement of navigation depended as much on the capacity to print, which Gutenberg had pioneered in 1449, as on new forms of calculation. For example, in sixteenth century England, an early innovation was to replace the oral instruction and reliance on memory which had characterised British navigation at sea, with books of charts, tables and sailing practices, an approach that the Dutch had already pioneered with the Spiegel der Zeevaert published in two parts over 1584–5. In England, when a copy was displayed in the Privy Council a decision was made to translate the document and modify it for use in England, with it duly appearing as The Mariners Mirrour in 1588.19 With an acceptance that seafaring could be assisted by printed aides it was only a matter of time for the desire to improve them to create a further demand for more accurate calculation of more useful navigational tables.
2.3 Competition at arms
The need for more accurate maps added to the demand for simpler ways of carrying out calculations. The defeat of the Armada at Gravelines during the (undeclared) Anglo-Spanish War of 1585–1604 provided a telling lesson in the sixteenth century of the importance of not only the economic power of merchant shipping, but also of the military importance of naval power. In particular it reinforced the need for manoeuvrable naval ships effectively utilising the best available gunnery.20
The use of cannon, muskets and pistols in warfare both on land and sea, had a history stretching back several centuries. But it had become a recognised feature of warfare by the mid-sixteenth century. So much was this so that King Henry VIII found himself troubled by shortage of gunpowder in his invasion of France in 1544 AD and had to import it.21
The early seventeenth century was a turbulent time comprising widespread conflict and upheaval across Europe. Indeed it was so turbulent as to comprise what some historians have referred to as “the General Crisis”,22 a time of confrontation, and in some places overthrow, of the legitimacy of the existing order, and more broadly, the relationships between state and society.23 Whether it was more profound than the Hundred Years War between France and England (1348–1453) or the Black Death which almost halved England’s population (1348–9)24 is hardly the point. It was a tumultuous time, and the tumult was widespread.
In England, just as an example, religious and political turmoil included: the schism between Rome and England under King Henry VIII between 1533–40, repression of “Papists” under Queen Elizabeth I (who established the English Protestant Church in 1559 and was declared a heretic by the Pope in 1570), further suppression under King James I, the Gunpowder Plot of 1605 in reaction to the treatment of Catholics, struggle in England between those in the House of Commons and King Charles I which ended in his execution in 1649 following the two English Civil Wars (1642–5 and 1648–9), rule by Oliver Cromwell as Lord Protector from 1653–8, and the subsequent restoration of the monarchy under King Charles II in 1660. But also across Europe, parts of the New World, and even beyond, it was a century of major wars and revolutionary upsurges, fertile ground for furious political machination and contest, and as it would turn out, innovation.
The increasingly widespread use of gun and cannon, in particular, provided a growing practical need to be able to calculate the trajectory of cannon balls and other projectiles. There was thus a demand for improved and more widely accessible methods of estimating all the relevant parameters (for example, matching quantity of powder required to wind, inclination and target, and projectile weight and type). By the early seventeenth century the search to solve these sorts of problems began to result in the development, explication, elaboration, popularisation, and with time, greater use ,of various helpful approaches to making the necessary calculations.
2.4 Managing in a more complex state and world
As already mentioned the Modern era was characterised by increasing flows of trade and finance between and within nations. Corresponding to this was the growth of cities, the increasing power of the state and merchants, and the growth across Europe of expanding bureaucracies as states attempted to regulate, control, and facilitate the powerful trends underway. Military conflict added to the pressure to wield collective force across kingdoms. Rulers in turn needed to plan, command, and control the collected forces. Consequently, as the Modern era developed, there emerged a virtual army of clerks, customs officials, excise officers, inspectors, quantity surveyors, architects, builders, and then technicians. These were assembled to form the apparatus of states as they sought to shape, manage, and control an ever more complex world. At the same time in the ever more complex organisations of commerce, a similar virtual army of employees was constructed to assist in the achievement of profit.25
Whether in the state, or the commercial sector, the need for calculation and the spread of the capacity to calculate became greater. Eventually that need would in part be met by the development of a host of calculational aids. But the pattern of change would not simply be one of invention following developing need. Rather those early insights and inventions aimed at aiding calculation, and even their deployment in practice, initially acted more as a prelude to deployment. It was only over a considerable period of time that the society began to understand that these tools of calculation could play a potentially vital role in the emerging work of state and corporation.
2.5 A growing fascination with mechanisation, and its increasing introduction into production.
The first developments in the technology of calculation in Early Modern Europe were perhaps as much cultural as economic in their motivation. In particular they reflected a growing fascination with the use of machinery. From the thirteenth century, windmills and the more reliable waterwheels (both of which had been known of since ancient Rome) began to be turned to an ever wider variety of productive purposes - from the traditional role of crushing grain, to cutting stone, blowing bellows in metal work, sharpening knives and weapons, sawing planks, printing ribbons, dressing leather, rolling copper plate, and much else.26 The productive value of machinery was becoming more widely recognised, as perhaps also was the enjoyment of the way it could extend human capacity and power. Indeed there is no reason to think that it would have been any less rewarding an experience to show off one’s new adaption of a water mill than it is to show off a new car or electronic device now. A quote from Walker (if set in pre-feminist language) sums up the way in which innovation is a product of a whole cultural as well as economic and technological system:
If calculation was to be used in practice, it had first to be understood to be useful in practical life. Similarly, if calculators were to be developed, then mechanisation had to be seen to be both appealing and potentially applicable. In relation to calculation, one key cultural development prefiguring its mechanisation, was the growing fascination with clocks and clockwork.
Cipolla points out that near the end of the thirteenth century people not only had a social use for knowing the hour, but could grasp the possibility and advantages of mechanising the measurement of time because they had already had experience with the mechanical extraction of work from wind and water. By the middle of the fifteenth century increasingly reliable mechanisms had been developed for clocks. Some became show-pieces in town towers. Over the next several hundred years clocks were miniaturised and clockwork became a mechanism for driving clocks, watches, and later music machines, dancing figures, moving pictures, and much more. So pervasive was the impact of clockwork that the universe and even the human body were reconceived as machines, of which God was the ultimate “clockmaker”.28 It will hardly come as a surprise, therefore, that we find that the first artisans to be employed by mathematical instrument makers would be clockmakers, and that the first calculator (as will be described later) was called a “calculating clock”.
3. Scaling the heights: New insights and proportional instruments
As the above suggests, a significant early pressure for assistance in calculation came from the combination of the need for more accurate navigation and the corresponding demand for better astronomical observation. Instruments such as the astrolabe and cross staff were used to measure the positions of the sun and stars. Charts and various tabulated information were used then to calculate the relationship between position and the observations. To gain greater accuracy errors in projection, parallax errors in observation, and the like began to be taken into account. The need for more accurate maps increased demand for finer capacity to draw to scale. Over the C17-C19 a steady process of innovation led to improved instruments assisting observation and calculation to meet these demands.
The measurement of distance had been aided by dividers (or “compasses”) at least since the Roman era. Below is a Roman pair of dividers from the C1 to C3 AD.

A pair of Roman 1st to 3rd century dividers (C1-C3 AD)
(collection Calculant)
From the C18 new instruments were developed building on that idea. A print of a drawing by Thomas Jefferys (~1710–1771) which shows a range of such instruments from the C18 is shown below.
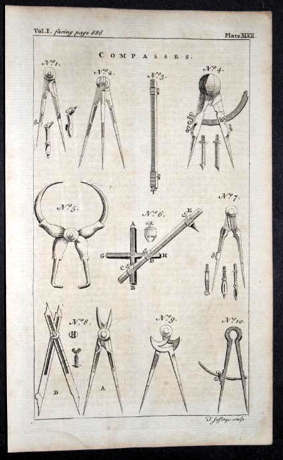
1710–71: Compasses by T. Jefferys sculp (Collection Calculant)
In this drawing, at the top can be seen the emerging shape of various compasses, constructed from brass and steel. Below, from this collection, is a typical pair of such dividers, also from the eighteenth century.

Two pairs of English eighteenth century dividers (~1740–1810)
(collection Calculant)
At the bottom left of this Jeffries print can be seen another device - a pair of dividers with a moveable central pivot. This instrument created a means of drawing distances to a particular scale. With one end marking an actual distance, the other could be reduced by a desired ratio by moving the position of the central pivot. An early reference to such a “proportional compass” was made by architect Daniel Speckle, as early as 1589.29 Dividers provided just part of the spectrum of mathematical tools that were under steady development. By the C18 such instruments were being produced in sets which included dividers, protractors, increasingly precisely scribed rulers, finer drawing pens, and other instruments, such as the proportional compass. The set of instruments, below, is from ~1880.
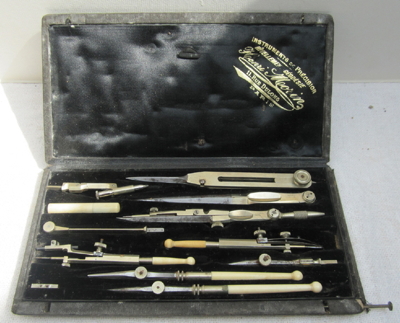
French drawing instruments ~1880 (including proportional dividers- top right)
(collection Calculant)
One mathematician - Thomas Hood - a Doctor of Physic from Cambridge University, took as part of his teaching task the design and documentation of potentially useful instruments. One instrument which he describes emerged naturally from the concepts of dividers, and proportional scaling inherent in the proportional compass. This was the sector - a set of dividers, but with flattened legs upon which could be marked various scales.30 It represented a considerable advance in aids to calculation.
3.1 The sector - an early calculating rule
Others (including Galileo Galilei) have claims to the invention of the sector.31 Hood first described his sector in 1598. Also known as a proportional compass the sector consisted of two rulers of equal length joined by a hinge and inscribed with various scales, to facilitate, in particular multiplication and division (but which could also be used to assist in problems of proportion, trigonometry, and calculations of square roots). It utilises the geometric principle, articulated by Euclid, that the like sides of similar triangles are in the same proportion. By forming an equilateral triangle with side and base in a particular ratio, multiplications in the same ratio could be read off for any other length of side allowed by the instrument.
Hood’s sector was constructed by Charles Whitwell, a fine instrument maker.32 However, the process of adoption was far from immediate. It was helped when, in 1607, Edmund Gunter, a young mathematician not long from his studies at Oxford, began to circulate his hand-written notes on The Description and Use of the Sector showing in particular how well it could be applied to the problems of navigation by Mercartor’s charts. In this he found support from Henry Briggs. In 1597, Briggs had been appointed as the first Gresham Professor of Geometry at Cambridge University with an aim of bringing geometry to within reach of the people of London.33 The very creation of this Chair indicated that there was a growing understanding of the potential utility of mathematical thinking. (However, the Chair was kept within the bounds of propriety by focussing on geometry which had less association with the “dark arts”). Briggs discharged his duty in popular education, amongst other things, by giving his lectures not only in the obligatory learned language of Latin, but repeating them in English in the afternoons. With Brigg’s support Gunter’s Use of The Sector was issued in print in 1623.
Sectors were in common use right through to the early twentieth century. Two sectors (from collection Calculant) are shown in Two Sectors below. The first is a Brass French Gunnery Sector from about 1700 by Michael Butterfield, Paris. Michael Butterfield, and English clock maker was born in 1635 and worked in Paris from ~1680 to 1724. The second is an Oxbone Architect’s Sector by T. and H. Doublett who practiced their craft in London around 1830.
 |  |
| Brass French Gunnery Sector | Oxbone Architect’s Sector |
| by Michael Butterfield ~1700 | by T. and H. Doublett ~1830 |
| (collection Calculant) | (collection Calculant) |
It is worth making a couple of observations about these sectors.
First, for reasons already mentioned, the learned designers of these early calculational aids seldom had the skills necessary to make them. Artisans, such as Michael Butterfield, who did have the highest relevant skills were frequently found amongst the members of the watch and clock makers guilds. Later specialist mathematical and scientific instrument makers (such as T. and H. Doublett) began to emerge.
Second, the construction of these aids required appropriate and available materials. For a gunner a robust brass sector made good practical sense. It needed to stay serviceable through the rigours of a battle. For an architect, 130 years later when sectors were being produced and used in larger number, the softer material of oxbone, which was both readily available and provided a white easily scribed ivory-like background for black engravings, created a much lighter instrument well suited to purpose.
The various scales which could be placed on sectors included trigonometric scales (e.g. sines and tangents) and linear scales for multiplication and division. To use these for multiplication and division one could, with a pair of dividers, set up a triangle of the required proportions.
John Robertson, in 1755, described the method thus: “To take a diſtance between the points of the compaſſes. Hold the compaſſes upright, ſet one point on one end of the dſtance to be taken, there let it reſt; and (as before ſhewn) extend the other point to the other end.”34
Using the same dividers, following the above, it was necessary to measure off the distance between the two “legs” of the sector at the required point along them.35 As can be seen from the dividers in this collection, the accuracy of calculations using sectors was limited by the fineness with which their scales were rendered and the precision with which the points of the dividers could be applied to the task of measuring them. The process was thus slow, inherently inaccurate, and required considerable dexterity and practice to achieve a credible result.
3.2 Napier and the challenges of multiplication and division.
For astronomical, and many other calculations, the sector was never going to provide adequate accuracy. Yet the only way to do these better, absent great skill with an abacus, was by laborious long multiplication and division on paper. Only an elite in any case had the mathematical literacy to carry such calculations out. Yet for those early mathematically literate people (for example, astronomers such as Kepler) the process was an enormously time consuming drudgery. There had to be a better way.
John Napier (1550–1617), Eighth Lord of Merchiston, was an imposing intellectual of his time. He pursued interests in astrology, theology, magic, physics and astronomy, methods of agriculture, and mathematics.36 If these seem a strange set of areas, it is to be remembered, as Stephen Snobelen reminds us also of Newton, that few people now: “…have an understanding of what an intellectual cross-road the early modern period was. In fact, we now know that Newton was in many ways a Renaissance man, working in theology, prophecy and alchemy, as well as mathematics, optics and physics. In short, neither Napier nor Newton who came after him was “a scientist in the modern sense.”37
Napier was an ardent Protestant. He wrote a stinging attack on the Papacy in what he would have regarded as his most important work.38 It was a great success, and was translated into several languages by European reformers.39 He also devoted considerable time to seeking to predict, on the basis of the Book of Revelation in the Bible, the likely timing of what was believed to be the coming apocalypse, which he concluded would come in 1688 or 1700. (At the time the “apocalypse” was not taken to mean so much the end of the world as the “temporary social disintegration and moral chaos, which is in turn mirrored in the devastation of nature.”.40) In any case, Napier did not live long enough to be confronted with the prediction’s failure. (Nor indeed did he need to confront the implications of Sir Isaac Newton’s musings, in 1704, based on similar numerological investigation of the Bible, that the apocalypse would be no earlier than 2060).41 Napier did however, live to see himself celebrated as the prodigiously gifted mathematician, and ingenious inventor, that he was.
In the course of his mathematical ‘hobby’ Napier invented an ingenious system of rods (now known as “Napier’s Rods” or “Napier’s Bones”) which could be manipulated to enable two numbers to be multiplied together with little mental effort, although some manipulation of the rods. A drawing of a set from 1797 is shown below. The mathematical principle had been described by Al-Khwarizmi in the ninth century and had later been brought to Europe by Fibionacci. It involved using a lattice of numbers for multiplication (essentially a way of writing down a multiplication table). But by breaking the columns of the lattice into 10 rods sitting neatly on a board Napier created a calculational aid which was considerably easier (although still somewhat tedious) to use. Napier described this invention in his book Rabdologiae - a word he created from the Greek for rod (rabdos) and calculation (logos) - which he published in 1617.42
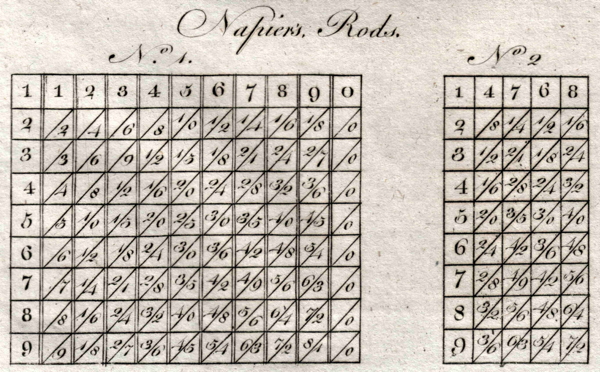
Depiction of Napier’s Rods, 1797.43 (collection Calculant)

Set of Napier’s Rods (of recent construction)
(collection Calculant)
The use of these rods can be illustrated by, say, multiplying 4 x 89. To do this read the 4 row of the last two rods (rod 8 and 9). Reading from right to left the right most digit in the result is 6 and 3 is carried. Moving left the next digit of the result is 2 to which the carried 3 must be added to give 5, with 3 to be carried. This then gave 356 as the result. This is no more than a simple way of replacing the multiplication tables that otherwise must be memorised. Pen and paper were still required especially if the multiplier was composed of more than one digit (e.g. 34 x 89), so that the process needed to be repeated for each of these (3×89 x10 + 4×89) then adding together these resulting “partial products”.
More importantly, after 20 years of work Napier also devised and had printed in 1614, a set of tables, Mirifici Logarithmorum Canonis Descriptio (“Description of the Marvellous Rule of Logarithms”). These enabled direct multiplication to be carried out through simple addition. It is from these that modern tables of logarithms (with some additional conceptual improvements) are derived. These are based on the fact that the powers of numbers add when the numbers are multiplied (i.e. 23x24=27). This fact had been known since the time of Archimedes. But it was Napier who thought to use this sort of property to tabulate numbers in terms of the power of some “base” (2 in this example). In fact, Napier did not achieve his tables quite in this way. Rather it is believed he started from an earlier approach using a property from trigonometry.44 This led him to a geometric argument based on the theory of proportions. Using this he constructed his functions.45
Napier’s tables were welcomed by mathematically minded scholars across Europe. Indeed the astronomer Keppler (1571–1630) noted that his ground breaking calculations in relation to Tycho Brahe’s astronomical observations would have been impossible without the use of the tables.46
Henry Briggs, the first Gresham Professor of Geometry at Cambridge (already mentioned) had travelled to meet Napier in Edinburgh in 1615. There it is reported the two men gazed in admiration at each other for a full quarter hour before finding words to speak.47 Briggs had suggested in a prior letter that it would be good to develop tables of logarithms to base 10. Napier who had had a similar idea was unable to do the work because of ill-health. He was however very pleased that Briggs might carry the work through.
Briggs did develop such tables of “common logarithms” the first of which gave the logarithms from 1 to 1000. It was published as a 16 page leaflet Logarithmorum Chilias Prima in 1617. His colleague Edmund Gunter at Gresham College published a more complete set from 1 to 20,000, in 1620. It was accurate to 14 decimal places.48 The usefulness of such tables for serious calculations involving multiplication, division, and powers of numbers to high levels of accuracy was clear to those who became familiar with them. That knowledge and the tables themselves, usually supplemented by corresponding tables for trigonometric functions, spread rapidly.
In 1625 Wingate published a French edition of Brigg’s latest tables. A year later in 1626, Dennis Henrion published his tables “Traicté de logarithms” (of which there is a copy in this collection, see below). Together with Wingate’s, these tables made available the power of logarithms across Europe.

1626: Traicté de logarithms by Dennis Henrion
(collection Calculant)
Tables of logarithms, improved in various ways over time, were published either by themselves (e.g. Tables by Gardiner, 1783), or in the context of “ready reckoners” (e.g. Ropp’s ready reckoner, 1892 , in this collection). Even up until the late C20 most school children were expected to have a passing understanding of how to use such logarithms prior to graduating to adult work. Extraordinarily useful as tables of logarithms were, a certain level of skill was required to use them. As many later in life would find, that skill also was not hard to forget. Tables of logarithms by Gardiner in 1783 are shown below.

1783: Tables Portatives de Logarithms by Gardiner
(collection Calculant)
The process of multiplying with logarithms could only be as accurate as the accuracy to which they were tabulated. Using them required a certain level of meticulous writing down of intermediate numbers and careful addition and subtraction. Using them was not easy for many people, and certainly not quick for even more. At a time when the need for ready calculation was spreading in the economy there was a growing potential, if not yet realised, demand for other developments that would reduce the time, effort and skill required. Yet even in the C17 with an expanding interest in calculation there was a place for something that would be quicker and easier, even if not so accurate - somewhere between a quick rough calculation and the painstaking methodology of logarithms.
3.3 Proportional Rulers: The Gunter Scale
Not only had Brigg’s colleague, Professor Edmund Gunter, published his Canon triangulorum in 1629, which contained logarithmic sines and tangents for every minute of arc in the quadrant to seven decimal places. In 1624 Gunter followed this with a collection of his mathematical works entitled The description and use of sector, the cross-staffe, and other instruments for such as are studious of mathematical practise. This work contained, amongst other things the detail of “Gunter’s scale” (or “Gunter’s rule”) which was a logarithmically divided scale able to be used for multiplication and division by measuring off lengths. It was thus the predecessor to the slide rule.49
In a second section (see below), the book details the design of a logarithmic proportional rule (derived from Gunter’s 1624 publication), along with additional explanations, charts and other elaborations (see below). The proportional rule could be used directly by means of a pair of dividers to measure off lengths corresponding to logarithms and thus to evaluate multiplications and divisions.
 |
| 1624: Graphical Construction of Gunter Scales |
| reproduced by Henrion 1626 |
| (collection Calculant) |
Gunter rules were usually equipped with both Gunter’s combination of a logarithmic and a linear scale. Often they also included a range of other scales (notably trigonometric scales for navigational tasks, such as required to work from elapsed time, speed and changes to compass bearing to distances travelled). In addition, important constants could be marked on them as “gauge marks”. Over the seventeenth century Gunter rules gained increasing acceptance and were used right through into the late nineteenth century. Some of the scales of a two foot long mid-nineteenth century navigational Gunter rule in this collection are shown below.
 |  |
| Logarithmic Scales of Gunter Rule | Navigational Scales |
| Gunter Rule (1831–1843) by Belcher & Bros | (collection Calculant) |
With its multiple scales (including the vital logarithmic scale) the Gunter rule was a lot more flexible in use than a Sector. It was much easier to make a rough calculation using it. All that was necessary was to measure off and add with dividers lengths against the various scales. This was much easier than having to write down the intermediate results. It was not long however before it was realised that instead of using dividers to add these lengths, the same thing could be achieved more easily by sliding two scales against each other.
3.4 The evolution of the slide rule
The initial insight was that the logarithms of two numbers could be added by sliding two Gunter scales against each other. There is however debate about who was the first to realise this.50 It was William Oughtred who published his design for a slide rule in 1632.
A series of designs followed. Three of these appear in Jacob Leupold’s book Theatrum Arithmetico-Geometricum51 of which Table XII (page 241), held in this collection, is shown in (i) in the Table below. (The top drawing is a design for a Gunter scale, and the two below are early designs for slide rules).52
In 1677 Henry Coggeshall desecribed a slide rule more like modern ones. Two rules with scales were held together with brass strips so one could slide past the other. This slide rule was found to have particular application for those who needed to do calculations quickly (and roughly) whilst on the job. In short it was a practical device for practical use.
One consequence of Britain’s increasing strength in shipping and maritime trade was that trade became an obvious target for revenue raising. During the C17 taxation was aggressively applied to offshore trade. The income raised was in part invested in the increased naval capacity and colonial infrastructure required to protect shipping. Tax was applied to commodities as diverse as glass, paper, soap, vinegar, famously tea, and of course alcohol in wine, ale and spirits (the taxation of which began in 1643). One consequence of this was that the quantities of these in diverse containers needed to be audited.53 This created a rapidly growing need for “gaugers” who could apply the mathematics of “stereometry” to estimating volumes of fluid held, and the corresponding alcoholic content. These measurements needed to be applied not only to barrels (whether on their side or standing), but also butts, pipes, tuns, firkins, puncheons and long-breakers (amongst other now long forgotten containers).54 Given the lack of widespread mathematical literacy, it was essential to have aids to enable gaugers to do this. Extensive manuals, tables and guides were published, but even so, it was clear to practitioners that they really needed something easier to use.
In 1683 Thomas Everard , an English Excise Officer (who is credited with introducing the term “sliding rule”), began promoting a new 1 inch square cross section slide rule with several slides for calculating excise.55 Shown in (ii), below, is an English four sided Everard pattern sliding rule from 1759. It includes various gauging points and conversions to square and cube roots for calculating volumes.56 In (iii) is a more modern looking slide rule shape, from 1821–84 by Joseph Long of London, also for use in gauging the amount of alcohol spirit in a container, and calculating the corresponding tax.
The slide rule evolved in what are early recognisable directions. The use of a hair line to read off multiple scales was suggested as early as 1675 by Sir Isaac Newton. Nevertheless, the introduction of a moveable cursor with this innovation included had to wait a century until a professor of mathematics, John Robertson, in 1775, added a mechanical cursor.57
It was Victor Mayer Amédée Mannheim, a Colonel in the French artillery and professor of geometry in Paris, who introduced the now familiar scale system, combined with a now fully functional cursor. This effectively brought together the key elements of what would become the modern slide-rule. He described it in a pamphlet published in 185158 An early slide rule made in 1893–98 by Tavernier-Gravet, but based on a pattern devised by Lenoir in 1814 (iv) is also shown, now fitted with a brass cursor. In (v) is a slide rule from about 1928 by the firm Keuffel and Esser with cursor and familiar scales. The Faber Castell 2/83N Novo Duplex slide rule (xii) with its multiple scales on both sides is often spoken of as the high point reached in elegance and utility of the straight slide rules. Production of it lasted until 1973 when electronic calculators rendered it obsolete. A progression of such slide rule designs is shown in Slide Rules below.
Over the late nineteenth and first half of the twentieth century a two-way innovation race began to achieve accuracy and capacity on the one hand, and compactness and versatility on the other. Greater accuracy required longer slide rules so they could be more finely divided. To overcome the practical difficulties American bridge engineer Edwin Thacher effectively chopped two 10 metre slide rules into 20 segments and set them side by side around in a cylindrical manner to form an open “cage” with forty scales and an equivalent length of 20 metres. The cage of scales could rotate around a fixed inner cylinder which bore corresponding scales. Compacted in this way the instrument (vii), which was patented in 1881, remained very bulky, but capable of multiplications and divisions to an accuracy of 4 to 5 decimal places. Professor Fuller subsequently developed a cylindrical slide rule (viii) which wrapped the scale around the cylinder in a spiral pattern giving a more compact instrument with a scale of equivalent length 12.7 metres, able to calculate to 3 to 4 decimal places. This was sufficiently practical to go into widespread use.
The search for compactness and versatility (at the cost of accuracy) continued resulting in a wide variety of circular pocket slide rules. Examples here are the the very first circular slide rule to be introduced in America, Palmer’s Computing Scale (vi), the Supremathic (ix), and the Fowler (x) - which combined a pocket watch style system with multiple scales. The Otis King pocket cylindrical slide rule (xi) was a particularly charming slide rule with its neat spiral scale design but of course less accurate than its bulkier predecessors, being equivalent to 1.7 metres in length. These are shown in Circular Scales below.
The above is notable for the extent to which the slide rule, in its multiple variants was able to be shaped into a tool of trade in multiple emerging and growing professions. Its advantage over logarithm tables was its speed of use at the expense of complete accuracy. As noted above, where equivalent accuracy was created the instrument became very large and clumsy.
3.5 Nomographs
We may add two further considerations to that of accuracy, and that is skill and speed. The slide rule was well designed for a professional, such as an engineer, who might have both facility in logarithms and the capacity to understand and evaluate equations. However, the increasing complexity of production called for employees with multiple skills and knowledge bases. Not all of these could be expected to be able to carry out necessary calculations from first principles. One approach to enabling them nevertheless to proceed was to provide tables of results. “Ready Reckoners” provided this sort of facility giving, for example, interest tables for the calculation of mortgages.
For more complex equations with multiple variables it was either train workers to evaluate the equations from first principles or find some other way of solving them. Nomography provided an approach to achieving this. This methodology was invented by Maurice d'Ocagne (1862–1938) in 1880 and was used through to the 1970s. Its principles are described in several good references.59 A simple example of the approach is given in below:
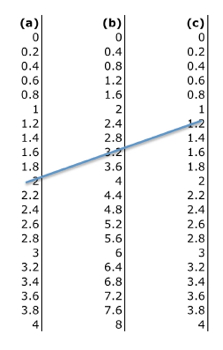
A simple nomograph for calculating the sum of two numbers (b=a+c)
This simple nomograph is used to add two numbers (one in column a) and the other (in column c).60 The properties of similar triangles give the result that a line drawn between the two numbers will cut the middle column (b) at the required sum. Since the outer scales may be logarithmic or trigonometric many more complicated expressions are able to be evaluated using this sort of approach.
Many nomographs were produced. Many were just printed on card allowing calculations to be read off using a rule as above. They were mostly if not invariably designed for a particular purpose.
It was also possible to create mechanical nomographs in which the scales were laid out and able to be read by turning pointers. Two devices which utilise these nomographic principles are shown below. The first is a Bloch Schnellkalulator from ~1924. The second is a Zeitermittler from ~1947. In both cases these are nomographic devices for calculating parameters required to cut metal with a lathe. The Bloch Schnellkalulator is notable for its use of a linked mechanism which enables the results of one calculation to be fed as the input to another.

Bloch Schnellkalulator
~1924
(collection Calculant)
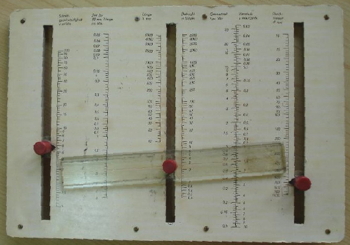
Der Zeitermittler
~1947
(collection Calculant)
3.6 Some Reflections
As the above suggests, multiple solutions were emerging to multiple formulations of the “problem of multiplication”. Each solution had its limitations, whether it be ease of use in different practical circumstances, or accuracy. Thus, although slide rules had apparent advantages over Gunter rules, and Gunter rules over sectors, none of these simply vanished once the other had been invented. As Robertson noted in 1775, Gunter rules had simply been added to sectors as available approaches.61 Indeed, as shown by the objects in this collection, Gunter rules and sectors continued to be used right up into the nineteenth century. Even to this day, nomographs, often represented now in the form of computer graphics, continue to be used for particular applications.62
This undermines the simple minded view of innovation as a linear process of invention and improvement. Rather, as in any transitional period, multiple strands of change were in motion. They were deflected or shaped along the way by different motivations and pressures. One of these pressures was simply intellectual conservatism. That included the usual suspicion of practical compromises by those privileged to be able to focus purely on intellectual pursuits. When Gunter applied for a chair in mathematics at Oxford he was rejected by the Warden of Merton College, Sir Henry Saville. The reason given was that his instruments were “mere tricks”.63 Rejected from Oxford Gunter took up the Gresham Chair at Cambridge University. As noted earlier, this position was dedicated to exposing mariners and others to the potential usefulness of mathematics. Somewhat later an Experimental Philosophy group would grow up at Oxford (and in 1672 would gain a Royal Charter from King Charles II and become the Royal Society).64
There is a range of other factors that would have affected the spread and adoption of a new instrument such as the slide rule. For example, in order to manufacture slide rules for mass distribution, the skills and techniques for scribing logarithmic scales would need to be picked up by potential instrument makers. Until many were produced and means were found to cheapen the process, costs of new instruments might well have been at a premium. Perhaps more important would have been the need to learn how to use them. The naval profession was not considered a place for scholars. Rather training was on the job and at the hands of senior sailors and officers. In short, whether in marine environments, or on land amongst architects, builders and planners, skills deemed necessary for doing the job were taught from master to apprentice in the age old fashion of the guilds. This was a very suitable way of passing on stable and established best practice. It was not necessarily so receptive to or good at transmitting new fangled ideas of scholarly gentlemen living and working in the privileged seclusion of universities. The Gresham Chair was intended to break through that, but it was too large a job to be achieved by any one such establishment.
The use of scaled functions to calculate (whether using principles of similar triangles, trigonometric relationships, or logarithmic properties), whether embodied in tables, or whether incorporated into instruments (such as sector, Gunter scale, or slide rule) had one key limitation. Apart from the logarithmic scale, the remaining scales or marks were generally about solving specific problems. These were problems such as how to multiply or divide by physical constants or how to work out trigonometric relationships and apply them to various problems. Almost all of the calculational aids available were limited in accuracy either by the scales used or number of decimal places to which tables could be listed. They did not provide in any useful way for addition and subtraction which many found challenging to do in their heads. And being focussed on specific problems, these aids lacked the generality (as well as accuracy) that might be required to solve the multiple diversifying calculational tasks of increasingly complex societies.
That there was a need for something new is clear with the clarity of hindsight, especially centuries later. But to cast the track of innovation simply as fulfilling an obvious need is too simplistic. As we have noted already, there were at least two (and probably many more) publics for whom innovation in mathematics might have relevance. But that does not mean that they recognised that relevance. And in any case mathematical inventions might have very different relevance to those publics. The two publics we have already identified were:
(i) those intellectuals (whether labelling themselves as philosophers, mathematicians or some other way) focussing on mathematical exploration, and those other natural philosophers including the emerging group of “experimental philosophers” who might utilise their work. For these there might be the delight of embodying mathematical ideas in devices, or in the case of what would become later known as scientists (for example, astronomers) the prospect of doing away with the tedium and delay of endless simple mathematical calculation.
(ii) the practitioners of practical arts - whether sailor, cartographer, or clerk who might appreciate a tool that would ease their work. Complementing this there was a slowly growing demand for larger numbers of “calculators” - that is, people who could calculate. Given that this was not a widespread skill, as already noted, anything that might ease the learning and teaching of the skills, or replace the need for it with some device, could over time prove attractive.
As Laird and Roux note, “The establishment of mechanical philosophy in the 17th century was a slow and complex process, profoundly upsetting the traditional boundaries of knowledge. It encompassed changing view on the scope and nature of natural philosophy, an appreciation of “vulgar” mechanical knowledge and skills, and the gradual replacement of a casual physics with mathematical explanations.”65 It was this slow and complex process that would eventually give rise to mechanised calculation. But as suggested above, the developments would be complex, many stranded, and over time increasingly tangle together the two worlds of the philosophical and practical arts.
4. Mechanical Calculation - first steps
As with much of mathematics, the interest in mechanisation of calculation was to some extent a re-discovery of similar interest several thousand years before. The Antikythera mechanism originating in ancient Greece has already been mentioned. It was, in a sense, a hand cranked calculator for predicting regular events such as celestial formations and important occasions of state. In ancient Rome, there had also been considerable use made of pumps, levers, wheels and gears, for a variety of uses in construction, and destruction - especially in the use of machines of war.
The Roman emphasis on the importance of transport for the state had led also to the use of measuring machines including the odometer of Heron of Alexandria - a device used to measure distance traversed by a rotating carriage wheel by coupling it to a system of incrementing gears. As described by Vitruvius (~15 BC),66 the rotation of the carriage wheel was measured by this device in units, tens, hundreds, thousands and tens of thousands of paces.67 This sort of counting mechanism could form a natural basis for the important “carry” mechanism (e.g. where 9+1 is converted to 10) of an adding machine. Still, for that potential to be capitalised upon there had to be a recollection or re-discovery of the sort of mechanism, and perhaps more importantly, an interest in constructing one. As already mentioned, the budding interest in mechanisation in the early C17 (building in particular on the widely understood appeal of the success of clocks, clockwork, and new mechanical insight about nature) provided an appropriately fertile base for that interest.
Given the increasingly multi-stranded stress on the importance of calculation, it is not surprising that at least some natural philosophers in the England and Europe took up the challenge of how best to facilitate it. Even though often distant from mundane economic or practical need there were intellectuals of the day who shared not only an enthusiasm for discovery, but also a growing enthusiasm for invention. It was only a matter of time before a growing interest in mechanisation would intersect with desire to simplify the process of calculating solutions to a variety of mathematical problems.
One group of such intellectuals were the Jesuit theologians who were now emerging as mathematical thinkers. By 1650 some 50 mathematical chairs had emerged in Jesuit colleges across Europe.68 It was Joannes Ciermans (1602–1648), a Flemish Jesuit, who in 1641 published one of the most comprehensive surviving courses covering geometry, arithmetic and optics. These were presented in a practical way, designed for his students who were mostly expected to become military officers.
In the “Problemata” for one week of his course, Ciermans noted slightly obscurely (loosely translated) that while many seek savings in multiplying and dividing the outcomes usually require more effort to do so than from first principles. However, he wrote, there is a method with “rotuli” (normally rolls of parchment for writing upon, but could also intend the more modern diminutive for rota i.e. little wheels) with indicators (or pointers), which enables multiplication and division to be done “with a little twist” so the work is shown without error.69
It is not clear if the device described by Ciermans existed, was envisaged, or was merely suggested. It is certainly not clear precisely how it would have worked. One could speculate, since Ciermans refers to both logarithms and rabdologiae, that it might have embodied some form of Napier’s rods on rolls. But it could have involved little wheels. It could just have been a way of checking accuracy by displaying the progress in a calculation using parchment rolls which progressively revealed each intermediate step. Indeed an improvement to method of this sort might well have provided greater improvement in arithmetic speed and accuracy than some more complicated mechanical approach. Tellingly this demonstrates how much may have been lost from the highly perishable historical record over four hundred years. Indeed, it was only in the last fifty years of the twentieth century that more tangible evidence did emerge that a quarter of a century before Cierman’s remarks a calculating machine had indeed been constructed using Napier’s rods set in rollers together with a mechanism for adding and subtracting based on the interaction of little wheels.
4.1 Schickard’s Calculating Clock
It is hardly surprising that the first steps towards innovation in the mechanisation of calculation would come from either someone who was from the nobility, or could draw on noble patronage, and with an established background (in commerce, church or state). This was practically a prerequisite to having had access to the education, adequate time and resources sufficient to enable such ideas to be worked out, and then implemented by employing the guild skills of clock makers or other skilled artisans.
The earliest of the known Modern attempts at mechanising calculation is that of Wilhelm Schickard (1592–1635). He was born in the German town of Herrenberg, near Tübingen, gained his first degree in 1609 and a Master degree in theology in 1611, and became a Lutheran minister in 1619. After a spell as professor of Hebrew at the University of Tübingen, in 1631 he was appointed to the University as professor of astronomy, mathematics and geodesy.70 Importantly he was an intellectual who had grasped the importance of applying his intellect beyond theory to practical matters. He was an accomplished engraver and cartographer and devoted considerable time to the first geodetic land survey of Württemberg.71
It is worth remembering the smallness of the circle of people who had the necessary skills, interests and resources to participate in what we now know of as science. The astronomer Johannes Kepler, who was instrumental in demonstrating that the planets might most simply be considered to move in ellipses around the sun, and who provided other crucial insights that would later inform the work of Newton, was a graduate of the University of Tübingen where he had studied under Magister Michael Maestlin, one of the leading astronomers of the time.72 It was through Maestlin that Kepler came to know of the still suppressed work of Copernicus for who’s solar-centric theory he became a strong supporter.73 His first book, Mysterium Cosmographicum, was published in Tübingen and it was presumably on one of his visits to Maestlin there that he was introduced to Schickard. They had much in common - both being mathematically gifted and knowledgeable, and both also sharing strong Lutheran theological interests.74
Schickard’s invention is revealed in two letters to Kepler and note to artisans, the first being in 1623, where he describes an “arithmeticum organum” (“arithmetical instrument”) that he has invented, but later as a Rechen Uhr (calculating clock) in a surviving note to the artisan constructing his machine.75 It is not known whether a complete Schickard’s “calculating clock” was ever actually built, although given he describes it operating, a prototype of the lower (adding machine) part was almost certainly built, and very probably a prototype of the whole was commissioned since he also ordered one for Kepler. Our knowledge is based on notes to artisans on building the machine, and drawings (see below) as well as comments to Kepler (discussed later). However, in his second letter Schickard made clear that he was not giving a full description.76 Surviving sketches are shown in Sketches by Schickard.
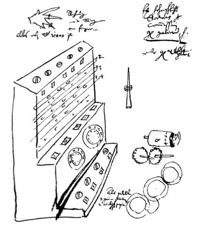 | 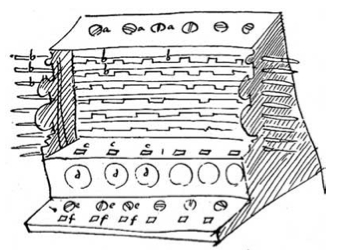 |
| Original sketch by Schickard ~162377 | Second sketch by Schickard78 |
The first replica was of Schickard’s device was constructed in 1960 by Professor Bruno, Baron von Freytag-Löringhoff of the University of Tübingen. The replica in this collection, shown below is more recent.79

Working replica of Schickard’s Calculating Clock (1623)
(collection Calculant)
Through twenty-first century eyes the principle of the machine was simple enough. It was primarily intended for addition, subtraction and multiplication. (Division was possible but difficult with this device).
The bottom of the machine was for adding and was itself a real innovation. All mechanical adding devices work by moving some object in proportion to the amount to be added. The simplest adding device is a “ruler” whose numbers are laid out uniformly along it. Two different distances corresponding to two different numbers can be added together and read off. Schickard utilised successive rotations of a wheel to add numbers, and perform the carry (9+1=10) in a manner reminiscent of an ancient Roman odometer.

Schickard front panel
(collection Calculant)
As can be seen in the replica above, a line of disks represented successive places (from the right units, tens, hundreds…). Behind the disk a gear wheel was turned which, when it passed from “9” to “0” engaged with the wheel to the left to move it by one unit. Adding was achieved by anti-clockwise rotations, subtraction by clockwise rotations. The set of knobs in the base allowed intermediate results to be recorded.
The vertical section at the top was a mechanical cylindrical embodiment of Napier’s bones (published six years earlier) to aid multiplication.

Schickard rear view showing Napier cylinders
(collection Calculant)
At least as interesting as the specifics is the mood of the moment. Schickard was a member of a small network of people spanning Europe and the UK (Napier in Scotland, Kepler and Schickard in what is now part of Germany) of somewhat different backgrounds. All were either resourced by inherited or institutional wealth (Napier), Kepler (under patronage of Emperor Rudoph II via Tyco Brahe) and Schickard (supported by the University). All were well educated in the classics and inspired by multiple and to an extent overlapping passions of theology, philosophy (including natural philosophy) and mathematics. And all now shared a sense of excitement that it might be possible to make break-throughs in systematic knowledge. The reward could include the pleasure of aiding each other to break new intellectual ground coupled with the pleasure of achievement, the glow of approval from each other, and perhaps not only the admiration but the possibility of continued or enhanced support from patrons.
The first European ‘scientific journal’ (Le Journal des sçavans - later Le Journal des savants) published its first edition on 5 January 1665. Once established, in 1666, it soon became the written forum for the Paris Academy of Sciences.81 (In England, the Philosophical Transactions of the Royal Society began publishing only three months later in March 1666.) Prior to that (indeed after, in many places) news of discoveries was spread by letters sent to trusted figures in the small ‘invisible college’ of thinkers. Thus, for example, William Oughtred (first to publish about the sliding part of the slide rule) was one of the key contact points in England. Others would learn of developments in the popular seminars he delivered at his home.82 The network was thus characterised by a shared excitement and objectives, a developing communication system, the stimulus of possible positive outcomes, and consequently a level of competition (as revealed in the often quite tense and hard fought battles beginning to rage over who had primacy in any particular insight or invention).
Kepler was greatly excited by the publication of logarithms which he utilised to greatly reduce the enormous calculational effort in his computations of The Rudolphine Tables and later works. He dedicated his Ephemerides to Napier in 1617.83 Professor Briggs (astronomer and geometrician) now at Gresham College, Cambridge, as mentioned earlier, was a close colleague of Napier and had written of his tables “…I never saw a book which pleased me better or made me more wonder”.84 He would later take Napier’s work further forward producing new tables of logarithms to base 10. In 1609 Briggs was also impatiently awaiting Kepler’s exposition on ellipses.85
Finally, of Schickard, Kepler wrote admiringly that he has “a fine mind and is a great friend of mathematics; … he is a very diligent mechanic and at the same time an expert on oriental languages.”86 It is known that Kepler and Schickard had discussed applications to astronomical calculation by Kepler of Napier’s logarithms and rods as early as 1617. This may well have inspired Schickard to find a mechanical embodiment of the rods.
On 20 September 1623 Schickard wrote to Kepler to tell him that:
In a second letter to Kepler, on 25 February 1624, Schickard notes that he had placed an order for Kepler for a machine. He notes that unfortunately when half finished the machine had fallen victim to a fire and the mechanic did not have time to produce a replacement soon.88
The most often noted deficiency of Schickard’s machine was in its “carry mechanism” (the mechanism that moves the displayed result from 09 to 10 when 1 is added). In Schickard’s design it seems that the “carry” was achieved every time an accumulator wheel rotated through a complete turn, by a single tooth catching on an intermediate wheel causing the next highest digit in the accumulator to be increased by one.
Carrying a number required extra rotational force to be applied (since more than one wheel had to be moved simultaneously). If, for example, 1 was to be added to a number like 99999 to give 100000, all of the wheels bearing a 9 would have to be moved by the force applied to the right hand wheel as it moved from 9 to 0. Unfortunately that would require so much force as to break the machine. In short, the adding part of the machine would jam if too many numbers had to be carried simultaneously.
In addition, the machine was not simple to use. The use of Napier’s rods to effect multiplication required considerable arithmetic knowledge - quite probably so much that the problem would more easily be done with pen and paper, or jetons and counting board. Probably Schickard’s idea never moved beyond the prototype stage. Nevertheless, it was an inventive start. And the dynamic of the times, which had led to it being conceived went beyond the circumstances of Schickard. A skein of motivations had contributed to it being a potentially rewarding moment for Schickard to explore the ways a “clock” might calculate. Regrettably, Wilhelm Schickard, his family, and thus his calculating clock, all fell victim to the plague that followed the Thirty Year war and his work slipped into obscurity for three hundred years.
At the heart of Schickard’s invention had been the idea of combining a convenient embodiment of the multiplication tables underlying Napier’s rods, with a device to assist in adding up the partial products. There would be other attempts at this approach to direct multiplication over the next three centuries, running right into the twentieth century. However, as we will see, all proved rather clumsy, and when not clumsy to use, complex to make. Perhaps more important had been Schickard’s insight that a series of interlinked gear wheels could be used to add and subtract, and furthermore, that a carry mechanism was possible.
It was this second focus which was to prove a more successful direction over the next several centuries. The time was ripe for thinking about the application of mechanisation to calculation. Its use to reduce the labour of addition was an attractive line of attack. Thus it was not surprising that only two decades after Schickard, a similar mechanical method of addition and subtraction (with some definite improvements) was rediscovered elsewhere - this time in France.
4.2 Blaise Pascal’s Pascaline.
Blaise Pascal (1623–1662) had been only a 13 years old, when Schickard died but had already showed both a strong interest and flair for mathematics. His father Etienne, was a reasonably good mathematician in his own right, of noble birth and reasonably well to do, and when Blaise was 19 years old, with an appointment by Cardinal Richelieu to “Commissioner deputed by His Majesty for the Imposition and Collection of Taxes in Upper Normandy”.89 The pressure of work involved was enormous and Blaise was needed to help out in the extraordinary effort involved in adding seemingly endless numbers as taxes were calculated, collected, paid and audited. As a consequence he turned what would prove to be his brilliant mathematical mind to the more practical task of constructing a mechanism to assist in addition. One of his heirs (chevalier Durant Pascal) would later claim that finding no artisan clever enough, Pascal himself trained himself with the skills to produce one of the machines with a few tools. However, this is very likely false. The clock-maker’s guild was well established in Rouen, clock-makers had all the necessary tools, and further had an exclusive right to make any machine like a clock.90 In any case, Pascal definitely did seek to wring the very best out the local artisans, and in this he is considered to have been very successful, producing machines which were not only useable, but works of the finest craftsmanship. A fully working replica of a Pascaline, crafted by Jan Meyer in Germany, and acquired for this collection in 2013, is shown below.

Working replica of a Pascaline,91 style ~1650
(collection Calculant)
As to the innovation in mechanism there is no evidence that Pascal had any knowledge of Schickard’s invention. Nevertheless it was clear that he too was infected with the growing understanding that his invention could now be turned to reducing labour in new ways. His Pascaline turned out to be an adding machine, rather like that in the base of Schickard’s clock, but with two important improvements (and one significant deficiency). As with the Schickard’s machine, numbers were added by turning disks with a stylus which in turn turned interlinked gears. Pascal however experimented with ways to improve the practical functioning of this. Various details of the Pascaline mechanism, including diagrams in this collection from the famous Encyclopédie ou Dictionnaire raisonné of Diderot and d’Alembert in 1759 are shown in Mechanism of the Pascaline below.
First, drawing firmly on the history of clock design, Pascal introduced gears which were minaturised versions of the “lantern gears” used in tower clocks and mills. These could withstand very great stresses and still operate smoothly. Second, he sought to achieve a carry mechanism which could operate even if many numbers needed to be carried at once (e.g. for 9999999+1 to give 10000000). He finally achieved this with a system where as each gear passed from 0 to 9 a fork-shaped weighted arm (the “sautoir”) on a pivot was slowly rotated upward. As the gear passed from 9 to 0 this weighted arm was then released to drop thrusting an attached lever forward to rotate the gear ahead of it by one unit.
 |  | |
| Pascaline Mechanism | Replica Pascaline mechanism | |
| diagram (1759) | with spoked lantern gears | |
| Diderot & d’Alembert93 | ||
| (collection Calculant) | (collection Calculant) | |
 |  | |
| Turret clock | Replica fork-shaped | |
| with lantern gears94 | carry mechanism | |
| from 1608 | (sautoir) | |
| (collection Calculant) | ||
A deficiency was that the carry mechanism did not allow the process of addition to be reversed. Instead when subtracting a rather clumsy system had to be used of adding ‘complementary numbers’ (where a number -x is represented by (10-x), with 10 subsequently being subtracted). This was assisted by a window shade which can be switched between showing numbers or their complements.
Unlike Schickard’s machine which is known only by documents, and which in reality would have had practical problems with the carry mechanism, Pascal sought to find profit from his invention. According to him he created some 50 of his calculators of varying design before settling on a final design. Some eight surviving Pascalines can be found in museums and private collections. He also documented his machine in a short pamphlet,95 achieved what in modern terms would be called a patent for his invention - a right awarded by the monarch to exclusive production of the invention (thereby over-riding the clock-maker guild’s claim to this) - and commissioned an agent (Prof. Gilles de Roberval) to sell it.96
Whilst Schickard’s machine could multiply directly (using its ingenious incorporation of Napier’s rods), Pascal’s machine (despite his claim that it could be used for all operations of arithmetic) was primarily useful for addition, and with some mental effort, subtraction (see calculating with the Pascaline). What I argue elsewhere? is a rather empty debate has at times erupted over whether Pascal or Schickard should be considered the more fitting candidate for ‘inventor of the modern calculator’.97 Nevertheless, it is Pascal’s machine which has been referred to with reverance down the following centuries, not the least because a significant number were produced, it was mechanically ingenious, and some survive. A woodcut from 1901 of an accounting Pascaline, similar to that in the Léon Parcé collection, is shown below. Other details of the mechanism design are shown here.
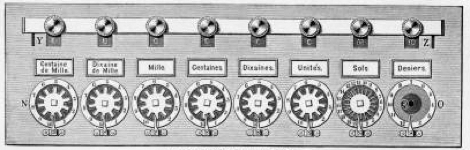
Wood engraved plate from 1901 depicting a Pascaline Calculator for accounting (~1642)
(collection Calculant)
4.3 Counting, Clocks, Colleagues and Courtly calculation
It is worth pausing to consider the reasons that Schickard and Pascal had launched into their geared calculator projects, almost certainly with no knowledge of each other’s efforts, being the first known such projects in more than 1500 years. Notably, whilst Schickard included a rendition of Napier’s rods to aid multiplication, and Pascal worked to create a more effective carry mechanism, both in rather similar ways ultimately sought to mechanise addition and subtraction through a set of interconnected gears and dials. Of course there was no single reason why they embarked on such a similar task so close together in historical time. Rather a skein of factors were coming together to make such innovations appealing and therefore more likely to be addressed by people with the resources and ingenuity to do so.
(i) Perhaps most subtly, this was a time when philosophical inquiry, and the emerging practice of what would more commonly become known as scientific inquiry, were taking a more practical turn. There was a growing realisation that investigation which engaged with the natural world though exploration of how it behaved, could yield rich results. Notable in leading this idea was Francis Bacon, who in 1620 had written his Novum Organum, a strong argument that systematic empirical engagement of this type, could not but result in “an improvement in man’s estate and an enlargement of his power over nature.”98 Implicit in this was a narrowing of the gap between science and technology, new ideas and application for betterment, and intellectual investigation, tools and technique. It was no less than a launch of “the idea of progress” which, as mentioned earlier, over subsequent centuries was to act as a reinforcing ideology for merchants and entrepreneurs, eventually helping sweep before them and the market much of the religious and customary authority of the aristocracy.99
(ii) As already noted, it was a time when clocks and clockwork were celebrated, with even the Universe being considered, at least metaphorically, as being a form of clockwork. And what clocks did was to count time. They used the rotational motion of geared wheels to count out seconds, minutes and hours, which were displayed on dials. The design required gears that could cycle (through 60 seconds or minutes) and during each cycle ‘carry forward’ a minute or hour. Whilst the approach adopted was a more incremental motion, the extension of such a mechanism to count units of 10s and carry did not require an impossible leap of insight. It is no coincidence, therefore, that Schickard named his device a ‘calculating clock’.
(iii) Artisans, skilled particularly in the art of constructing clock mechanisms, existed with tools and workshops that could be turned to the task of constructing, similar, if differently configured and designed gear trains, dials and associated components. As already remarked, the importance of clocks is reflected in Pascal’s choice of lantern gears for his Pascaline. Even his famous sautoir, whilst highly innovative and different in form, is reminiscent of both the Verge escapement mechanism introduced into clocks from the late thirteenth century and even more in the remontoire gravity powered mechanism invented by Jost Burgi (1552–1631) in about 1595. In both of these, as with the Pascaline, a toothed mechanism was mechanically ‘wound up’ in a cycle and releasing at the correct moment in the cycle to control, and in the case of the Remontoire power by a falling weight, the motion of connected parts.100
This important relationship between inventor and artisan was subtle. As the above suggests, the guild that knew all about gear trains that could count seconds, hours, and even days and months, was the guild of clockmakers. Inevitably they would be called upon in the construction of different counting machines, and inevitably they would have insights to contribute. History would know primarily of the class of “inventors” who had the power and status to commission, purchase the skill of the artisans, and announce the outcome of their work. But this is a symptom more of what is visible in history than a faithful reflection of the process of invention at the time. Inevitably these came about as a partnership between artisan and intellectual through a process mostly obscured by the barriers of class at the time, and the obscuring passage of passing centuries.
(iv) Of those now acknowledged as the “inventor” each had not only great intellectual ability but also a wide ranging intellectual curiosity. Combined with this was personal motivation to seek to mechanise calculation. For Schickard it was an increasing interest in discovery and application of new knowledge, found in a dispersed, small, but communicating network of people interested in all manners of philosophy and theology. It included natural philosophers such as Kepler, who had an increasing need to utilise and overcome the drudgery of large numbers of calculation. Napier through his rods and logarithms, had provided means to greatly assist multiplication. But reducing the drudgery of associated additions and subtractions was emerging as something that would be valued. Pascal’s initial motivation was to assist his father in his extensive revenue collecting duties. But Pascal was also on a rapid rise as a natural philosopher and thinker in his own right, where the devising of a ground breaking mathematical instrument also stood to be valued by the network of other thinkers in which he and Schickard were participating.
(v) The network in which Schickard and Pascal engaged was could not be composed, in any case, of any people. They had to be well educated and with time to follow these pursuits. And that required that, almost without exception, they would be well connected to, or members of, the highest ranks in society, that is the nobility. From this point of view, the products of their work were likely to be intended to find favour with others of that rank.
Consistent with this, many of Pascal’s machines would end up, not in the hands of practitioners of mathematically intense duties, but as curiosities on the shelves and in the cabinets of persons of eminence. The names indicating the provenance of some of the surviving Pascalines - Queen of Sweden, Chancelier Séguier, Queen of Poland, Chevalier Durant-Pascal - are consistent with this. But perhaps equally so is the beautiful workmanship and decorative working of materials which are characteristic of these instruments.
In a fascinating thesis,101 and subsequent published book chapter,102 Jean-François Gauvin develops a multi-stranded analysis of the role of scientific instruments, including the Pascaline, and their creators and use in the seventeenth century. Key to this are conflicts and resonances between continuities in cultural habit, and social, philosophical and ideological challenges to them that were beginning to gain force at the time.
Challenges such as Bacon’s Novum Organum reflected the beginnings of a discomfort with knowledge founded on the verities of ancient Greek knowledge, church orthodoxy and aristocratic tradition. Of course both Schickard and Pascal, sought and enjoyed the indulgence and support of aristocratic and religious sponsors and Pascal in particular would use his machines as much as a way of attracting that as for any commercial gain. But the transformation reflected in Bacon’s call was to progressively reposition the man of substance (a “gentleman”, or in France “l'honnête homme”)103 in relation to some tools such as these. Building on the existing prestige of clockwork and the growing understanding that intellectual advance was tied to mechanical engagement with the natural world, these devices could be seen to potentially restore the separation of the intellectual world of l'honnête homme from the drudgery of the ‘mechanical’ act of routine calculation.
Having said that, the machines were expensive (about of a third of a year’s average wages of the time).104 Pascal in his surviving Advice on the use of the Pascaline promised that the machine could “perform without any effort whatsoever all the arithmetical operations that had so often worn out one's mind by means of the plume and the jetons”.105 But in truth the use of it required a good knowledge of arithmetic to be used effectively (especially for division and multiplication, but even for subtraction). At best it was a mechanical substitute for what otherwise would have to be written down, save that it could perform addition with a little practice, and simple subtraction (where the result was not negative) with a little more. As Balthazaar Gerbier described the Pascaline in a letter to Samuel Hartlib in 1648:
But like rare books need not be read to add luster to the shelf, the machines needed not necessarily be used to add something to the owner. Basic mathematical skills were far from universally held, even amongst the nobility, and certainly amongst gentlemen. From this point of view, even if one could not add and subtract reliably in one’s head, let alone multiply using jeton (calculi) and pen, the potential allure of such a calculating machine was that by owning it, one could come to at least be seen to have an intimacy with such literacy. In these senses, as Gauvin argues, “Even though Pascal invented the machine to alleviate his father’s headaches as a royal tax collector, financiers and merchants, who tallied large amount of numbers, were not especially in Pascal’s mind. The pascaline was more than a mechanical contraption useful for business: used properly, it could bestow l'honnête.”107
Even so, despite Pascal’s best efforts, in particular stressing the similar complexity of the mechanism of his machine and precision required of its workmanship to that esteemed in clocks and watches, the Pascaline found no broad market. As Gauvin, puts it “Unlike watches, the pascaline was much heavier and thus not easily portable; unlike table-top clocks, it was not as ornate and could not do anything on its own. The pascaline was a luxury item that fit no preestablished fashionable categories and could not initiate by itself a new one. It became a rarity, and like most rarities it found its place in cabinets of curiosities.”108
The above provides some basis for understanding what followed: a series of developments and experiments in mechanical calculation, few of them seen abstractly providing much real advantage over traditional pen and jeton for doing arithmetic, but each embodied in beautifully worked prototypes, often frequently being found on the shelves or in the cabinets of curiosities of the nobility and others of standing, whether in Germany, France or England. Since details of these are available elsewhere109 we will rely on objects documented in this collection to simply act as signposts. In particular, two inventors following Pascal, Leibniz and Morland, will be briefly considered, each of which illustrates substantially the above contention.
4.4 The inventions of Morland and Leibniz.
The multiple potential attractions of such mechanical embodiments of arithmetic can be seen to be at work over the next several centuries. From Schickard and Pascal other inventors sought in one way or another to make progress over the known work, at least of Pascal. One of these was Leibniz in Germany, and the other Morland who created the first English calculator. Each made a further contribution to the art and whilst the practicality of their inventions, even at the time, remains in contention, each gained satisfaction from their efforts for one or more of the diverse reasons mentioned above.
Samuel Morland (1625–95) - son of an English clergyman - had a complex life in a difficult time. At the age of 24 (the year he matriculated from Cambridge) he experienced the English revolution with the execution of King Charles I. Then he began work for Cromwell as a courtier-inventor a year later primarily providing intelligence through methods of postal espionage (intercepting, opening, decrypting and interpreting, and re-sealing mail). In the course of this, he was almost killed by Cromwell on suspicion of overhearing a plot to lure to England and kill the exiled Charles II,110 son of the executed King Charles I. Indeed Morland had overheard the plot and subsequently reported it to Charles II’s supporters. After Cromwell’s death (in 1658) Morland was able to manage the delicate transition to service under the newly restored King Charles II and was knighted by him in 1660 and made a Baronet soon after.111
In the course of these events Morland, whilst certainly comfortably provided for (not the least after he married a Baroness), complained of the failure of his positions to yield wealth saying: 'Now finding myself disappoynted of all preferment and of any real estate, I betook myself too the Mathematicks, and Experiments such as I found pleased the King's Fancy.'112 On the basis of his mastery of engineering (in particular, fluid systems) Morland was eventually granted a newly created position of “Master of Mechanicks” to the King, and later was made a gentleman of his Majesty’s privy chamber.113 His inventions, thus played a two-fold role, first in his search to establish a role for himself in the context of the new Court, and second to supplement his wealth by seeking commercial success. In particular, he hoped for a lucrative outcome to devising mathematical instruments and selling them.
Morland had already seen a Pascaline, probably when on a diplomatic mission to Queen Christina of Sweden, a supporter of the sciences who in 1649 had been presented with a Pascaline (similar in looks and identical in function to the replica in this collection).114 He had also taken part in a diplomatic mission during which he stopped off at the court of Louis XIV for over a month, so he may well have learned more of the Pascaline, and made contact with scholars and associated mechanics at that time.115 He was thus aware of the potential allure of such inventions. Over the next few years he devised three different calculator designs: an adding machine (see below), a multiplying device (see also below), and an instrument with moveable arms for determining trigonometric relations. Several examples of Morland’s calculating devices are still in existence, in particular in museums in London and Italy. Not only did Morland design the machines but he wrote a book on the use of the instruments. Published in 1672 this can be considered the first known English language (and arguably the earliest surviving) ‘computer manual’. (A copy of this rare book, shown below, is in this collection).
 |  |
| Morland 1672 cover page | Morland 1672 multiplying instrument |
| “Instrument for Addition and Subtraction…” | (collection Calculant) |

Morland Adding Machine
adapted to the then Italian currency
(Istituto e Museo di Storia della Scienza, Florence - Photos by Calculant)

Morland Multiplying Instrument
(Istituto e Museo di Storia della Scienza, Florence - Photos by Calculant)
In essence the adding machine was a simplified adaptation of the Pascaline’s dials (turned by stylus), but without any carry mechanism (so that carrying had to be done by hand). Adding (or subtraction by an opposite rotation) was input through the larger wheels. Each larger wheel engaged with the small wheel above to register a rotation and thus accumulated a 1 to be carried. As with the Pascaline different input wheels were provided for different units (whether units, tens, hundreds, etc, or pounds, shillings and pence).
The multiplying machine was simply a mechanised representation of Napier’s rods. In this sense it followed in the footsteps of Schickard although it is doubtful that Morland would have known of Schickard’s work. In Morland’s machine the ten Napier rods were replaced by ten rotatable disks, with the corresponding Napier numbers inscribed on their circumferences (with units and tens of the rods placed diametrically opposite each other). To multiply the operator took the disks corresponding to the number to be multiplied, and lifted the lower windows plate, to placed the disks on posts. A key was then turned until a sliding indicator matched the multiplier (being a number from 1 to 9). Each turn of the key rotated the discs and advanced them under the windows producing a display of the partial products of the multiplier. The partial products then had to be added which Morland suggested could be done with the aid of his adding machine.116
These machines were variously received as “those incomparable Instruments”(Sir Jonas Moore),117 “not very useful” (Henri Justel),118 or “very silly” (Robert Hook).119 But in terms of obtaining patronage on the one hand (not only in England but also from the Medici in Italy), and at least some sales to those men and women with wealth but not much knowledge of addition or the multiplication tables, the instruments served at least some of the needs of their inventor. That being so, they perhaps provided more reward to both maker and purchaser in terms of status than they returned financial benefit for the former, or enhanced arithmetic capability for the latter.
Gottfried Wilhelm Leibniz (1646–1716) had a life filled with so many ambitions, such high profile conflict, and so much capacity that his biography can seem overwhelming. He has been described as “…an indefatigable worker, a universal letter writer (he had more than 600 correspondents), a patriot and cosmopolitan, a great scientist, and one of the most powerful spirits of Western civilisation.”120 At the same time his irascible personality was such that by the time he died, his contemporaries were said to feel a sense of relief and only his secretary attended his funeral.121 His father was a professor of moral philosophy who died when Leibniz was only six years old, but he grew up in the surroundings of his father’s imposing library from which he derived much satisfaction. He gained his Doctorate of Laws (on De Casibus Perplexis, i.e. On Perplexing Cases) at the age of 20 from the University of Altdorf in Nürnberg.
The scope of Leibniz’s subsequent work was extraordinary encompassing poetry and literature, law, political diplomacy, work to unify all knowledge in part by bringing the scientific societies together, a similar desire to bridge the gap between the Lutheran and Catholic church in particular, and all churches in general, and more enduringly, his powerful initiatives in science and mathematics. The products of his work in mathematics included the development of binary arithmetic, methods of solving systems of linear equations, and either the discovery of calculus (priority in this was contested by Newton) or at least the modern notation used for it. Central to his work was a belief that if a logically defined (‘mechanical’) algebra of thought could be developed then truths could be automatically generated and proved. (This quest can be found stretching back to the Stoics, and forward to the later work of Gottlob Frege, George Boole, Bertrand Russell, Kurt Gödel and many others). Given this enticing objective it is not surprising that, having heard of Pascal’s calculating machine when he visited Paris in 1672 on a diplomatic mission (later to be elected to the French Academy of Sciences), Leibniz decided to turn his hand also to creating a calculating machine.122
Almost certainly Leibniz did not have a chance to use a Pascaline or he would have discovered that an early idea that he had, to automate multiplication by placing a mechanism on top of the Pascaline to simultaneously move its input “star wheels”, would conflict with the machine’s internal mechanism. His second attempt was much more original. Although unlike Pascal he was never able to properly automate the carry system, he developed a machine which could more faithfully replicate the pen and paper methods not only of addition, but subtraction, multiplication, and with some ingenuity, division. The first and most enduring innovation was a new way to input numbers by setting an accumulating cog to engage with a “stepped drum”.
The drum had 9 radial splines of incrementally increasing length and could be turned with a crank handle. An accumulating cog could be slid along an axle parallel to the drum and when the drum turned through a full rotation depending on where the cog engaged with the splines of the drum,the cog would be turned by anything from 0 to 9 of the drum’s splines thus accumulating 0 to 9 units of rotation. An example from a C20 calculator is shown below.

Twentieth Century step drum following the same principle as Leibniz’s conception
123
Several such accumulating cogs with their drums were put side by side, corresponding to units, tens, hundreds, etc, and once a number was set (e.g. 239) it could be multiplied (e.g. by 4) by turning the crank through a full rotation the corresponding number of times (thus adding 239 to itself 4 times to give 956). The capacity to add a multi digit number to itself repeatedly gave the machine the capacity to multiply by simply turning a handle, which was a considerable advance over the Pascaline. Further, the crank could be rotated in the opposite direction to produce a subtraction.
As with Morland’s multiplication machine it was now possible to introduce a carriage which would be mechanically advanced (by means of a second crank handle at the end of a screw thread) to allow multiplication by more than single digit numbers to take place. The Pascaline had had no such mechanism and so the equivalent had had to be done by recording intermediate results with pen and paper. The deficiency in Leibniz’s machine, however, as already indicated, was that unlike the Pascaline, Leibniz had been unable to devise a robust carry mechanism able to handle either multiple carries across several output dials at once. As a result, the machine was far from perfected. It seems that only one was made in 1674 (by M. Olivier, a French clockmaker, working under instruction from Leibniz), that a few years later it was sent Herr Kastner in Göttingen (Lower Saxony) for repairs, and was later stored in an attic at Göttingen University where it was not recovered for 200 years. A diagram of the Leibniz calculator from 1901 is shown below, and the actual surviving machine is shown below.

Wood engraved plate from 1901 depicting the Leibniz Calculator (1673)
(collection Calculant)

Surviving Leibniz Calculator recovered from the attic of Göttingen University. Reproduced with permission from the Gottfried Wilhelm Leibniz Bibliothek.
4.5 The road forward
Multiplication tables and various tabluated functions (notably logarithms and trigonometric tables), and various physical embodiments of those notably in various forms of Napier’s rods, sectors and scales, would increase in use as need and access to education in their use broadened. But could a machine be constructed that would make the mathematical literacy required in the use of these, and traditional methods of arithmetic using pen, paper, and calculi obsolete? Clearly the answer was “not yet”.
Leibniz’s machine formed the final piece of a tryptage (with Pascal and Schickard) of foundation pioneering seventeenth century mechanical calculators. Together these constituted foundation stones in the subsequent development of a wide range of other calculational technologies over the next two centuries. Progressively these overcame many of the more apparent limitations in these foundation devices, yet they shared also one other characteristic. Despite hopes that may have been held by their inventors, none of them proved to be more than prototypes in the sense that their destiny would be as curiosities of great interest, perhaps prized by the few who might get hold of one, but for a variety of reasons (cost, capabilities, ease of use) of little broader practical importance. The reasons we have canvassed for constructing them, and possessing them, would remain pertinent, but the other possibility, that they might be cheap enough and be sufficiently intuitive in use to create a notable increase in mathematical facility in a widening group of users, would remain a dream, not to be realised, until Thomas de Colmar, two centuries after Leibniz, also utilised the step drum to open the door to the commercial production and widening public use of mechanical calculators.
« Part 1 Origins | | Part 3 The Late Modern Period (1800-) »
1 Joseph Camilleri and Jim Falk, Worlds in Transition: Evolving Governance Across a Stressed Planet, Edward Elgar, UK, 2009 (↑)
2 Francis Pierrepont Barnard, The Casting-Counter and the Counting-Board: Chapter in the History of Numismatics and Early Arithmetic, Clarendon Press, Oxford, 1916, p. 87. (↑)
3 From Gregorius Reisch, Margarita philosophica nova Anastatic, 1503, reprint with an introduction (in Italian) by Lucia Andreini, Salzburg: Institut für Anglistik und Amerikanistik, Universität Salzburg, 2002 (3 vol.). (↑)
4 see for example, Dan K. Bell, “Calculating with Calculi: the Counting Board and Its Use in Reckoning in Medieval Europe”, Proceedings of the AMATYC 31st Annual Conference, San Diego, California, 2005, pp. 20–35. http://www.amatyc.org/, viewed 10 July 2013. (↑)
5 Ibid pp. 40–49. (↑)
6 Barnard, The Casting-Counter, jeton 69, p. 203. (↑)
7 for an accessible rendition of this see, for example, E. K. Hunt and Howard J. Sherman, Economics: Introduction to Traditional and Radical Views, Second Edition, Harper & Row, New York, 1972. (↑)
8 Hunt and Sherman, Economics, pp. 52–3. (↑)
9 estimated in terms of the percentage of families. (↑)
10 Carlo M. Cipolla, Before the Industrial Revolution: European Society and Economy, 1000–1700, W.W. Norton and Company, USA, 1976, p.13. (↑)
11 Johannes Kepler, Astronomia Nova, 1609 (↑)
12 for a much more sophisticated rendition of the history of this concept see Bury, The Idea of Progress. (↑)
13 J.B. Bury, The Idea of Progress: An Inquiry Into Its Origin and Growth, 1920, reprinted, The Echo Library, UK, 2010, p. 23 (↑)
14 H. Spencer Jones, “Foreword by The Astronomer Royal”, in E. G. R. Taylor,The Mathematical Practioners of Tudor & Stuart England 1485–1714, Cambridge University Press, Cambridge, UK, 1954, p. ix. (↑)
15 J. Arbuthnot, “An Essay on the Usefulness of Mathematical Learning in a Letter from a Gentleman”, 25 Nov 1700, quoted in Taylor, The Mathematical Practioners of Tudor & Stuart England, p. 3. (↑)
16 Carlo M. Cipolla, Before the Industrial Revolution: European Society and Economy, 1000–1700, W.W. Norton and Company, USA, 1976, p.167. (↑)
17 Hunt and Sherman, Economics, pp. 23–4 (↑)
18 Larry Neal, International Capital Markets in the Age of Reason, Cambridge University Press, UK, 1990, p. 4 (↑)
19 Taylor, The Mathematical Practioners of Tudor & Stuart England, p. 41. (↑)
20 see for example, Aubrey N. Newman, David T. Johnson, P.M. Jones, “The Eighteenth Century”, Annual Bulletin of Historical Literature Vol. 69, Issue 1, 1985, 93–109 cited in http://en.wikipedia.org/wiki/Spanish_Armada#cite_note-25, viewed 15 April 2012 (↑)
21 Wayne Cocroft, Dangerous Energy: The archaeology of gunpowder and military explosives manufacture, English Heritage, Swindon, 2000, Chapter 1. (↑)
22 notably used by Eric Hobsbawm in two articles: “The Crisis of the Seventeenth Century”, Past and Present, issue 5 and issue 6, 1954. (↑)
23 Hugh Trevor-Roper, “The General Crisis of the Seventeenth Century”, Past and Present, vol. 16, 1959, p. 51. (↑)
24 Hunt and Sherman, Economics, p. 21 (↑)
25 for more on this see Camilleri and Falk, Worlds in Transition (↑)
26 Cipolla, Before the Industrial Revolution, pp. 150–65. (↑)
27 P. G. Walker, “The Origins of the Machine Age”, History Today, Vol. 16, 1966, pp. 591–92, cited in Cipolla, Before the Industrial Revolution, p. 171. (↑)
28 ibid, pp. 170–2 (↑)
29 Daniel Speckle, Military Architecture, Strasburg, 1589 cited in John Robertson, A Treatise of Mathematical Instruments, Third Edition, 1775, reprinted Flower-de-Luce Books, Virgina, 2002, p. vii. (↑)
30 Taylor, The Mathematical Practioners of Tudor & Stuart England, p. 41. (↑)
31 for a picture of Galileo’s made in about 1604, see http://en.wikipedia.org/wiki/Sector_, viewed 14 April 2012. (↑)
32 Taylor, The Mathematical Practioners of Tudor & Stuart England, p. 41. (↑)
33 ibid, p. 54, 184 (↑)
34 John Robertson, A Treatise of Mathematical Instruments As are usually put into a Portable Case, Reprint of the Third Edition, 1775, Flower-de-Luce Books, The Invisible College Press, Virginia, USA, 2002. p. 6. (↑)
35 see for example, Edmund Stone, The description, nature and general use, of the sector and plain-scale,: briefly and plainly laid down.,Printed for Tho. Wright and sold by Tho. Heath mathematical instrument maker, next to the Fountain Tavern in the Strand., 1721, especially chapter IV, available from http://books.google.com.au/books/about/The_description_nature_and_general_use_o.html?id=nqU2AAAAMAAJ&redir_esc=y (↑)
36 Mark Napier, Esq, Memoirs of John Napier of Merchiston: Lineage, Life and Times with a History of the Invention of Logarithms, William Blackwood, Edinburgh, 1834. (↑)
37 Stephen D. Snobelen, "A time and times and the dividing of time": Isaac Newton, the Apocalypse and 2060 A.D., History of Science and Technology Programme, University of King's College, Halifax, undated, http://www.isaac-newton.org/newton_2060.htm, viewed 22 April 2012. (↑)
38 John Napier, A Plaine Discovery of the Whole Revelation of St. John, 1593. (↑)
39 William F. Hawkins, “The Mathematical Work of John Napier (1550–1617), Bulletin of the Australian Mathematical Society, Vol. 26, 1982, p. 455. (↑)
40 Snobelen, “A time and times”. (↑)
41 ibid (↑)
42 A copy of this book is available for download from this site’s e-library. (↑)
43 Encyclopaedia Britannica, 3rd Edition, 1797, plate CCCXLIV, Andrew Bell copperlplate. collection Calculant. (↑)
44 namely sin(x)sin(y)=0.5{cos(x-y)-cos(x+y)} which as can be seen, also converts a multiplication into an addition of two terms (one negative). (↑)
45 see for example, Denis Roegel, Napier's ideal construction of the logarithms, 12 November 2011, http://locomat.loria.fr/napier/napier1619construction.pdf, viewed 19 April 2012 (↑)
46 Hawkins, “The Mathematical Work of John Napier, p. 456. (↑)
47 G A Gibson, Napier and the invention of logarithms, in E M Horsburgh (ed.), Napier Tercentenary Celebration : Handbook of the exhibition, Edinburgh, 1914, pp. 1–16, cited in J. J. O’Connor and E. F. Robertson, “John Napier”, St. Andrews College, http://www-history.mcs.st-andrews.ac.uk/Biographies/Napier.html, viewed 14 Dec 2011. (↑)
48 ibid (↑)
49 http://en.wikipedia.org/wiki/Edmund_Gunter - see also http://www.livres-rares.com/livres/HENRION_Denis-_Traicte_des_Logarithmes-95656.asp (↑)
50 See for example, Dieter von Jezierski, Slide Rules: A Journey Through Three Centuries, Astragal Press, New Jersey, USA, pp. 7–8, and Florian Cajori, The History of the Logarithmic Rule (↑)
51 A scanned version of this book may be downloaded from http://ia600304.us.archive.org/33/items/theatrumarithmet00leup/theatrumarithmet00leup.pdf (viewed 3 Jan 2012) (↑)
52 This page was held in a German family and placed on auction on ebay in January 2012 after the seller’s grandfather, an art collector, who had held it and had it restored, passed away. (↑)
53 Tom Wyman, “Kilderkins, Hogsheads & Dipping Rods: A Brief History of the Slide Rule”, Journal of the Oughtred Society, Special Issue 2007, pp. 19–26. (↑)
54 ibid (↑)
55 Wyman, “Kilderkins, Hogsheads & Dipping Rods”, p. 21. (↑)
56 The method of use is described in I. Rawbone, The Royal Gauger, Oxon, London, 1750 (↑)
57 Dieter von Jezierski, The History of the Slide Rule, Abstract Press, New Jersey USA, 2000, p. 11. (↑)
58 A. Mannheim, Règle à calculus modifiée, Grande imprimerie Forezlenne, Septembre 1851. http://www.linealis.org/IMG/pdf/Mannheim.pdf viewed 24 June 2012; Jezierski, The History of the Slide Rule, p. 12. (↑)
59 eg. Ron Doerfler, “The Lost Art of Nomography”, The UMAP Journal, Vol 30, No. 4, 2009, pp. 457–94; downloadable from http://myreckonings.com/wordpress/wp-content/uploads/JournalArticle/The_Lost_Art_of_Nomography.pdf viewed 11 July 2012 elegantly outlines the basic principles. Carl Runge, Graphical Methods, Columbia University Press, New York, 1912; readable online at http://www.archive.org/stream/graphmethods00rungrich#page/n0/mode/2up viewed 11 July 2012 provides an excellent overview of the relevant graphical methods for solving equations of many sorts. (↑)
60 A similar example is given in Raymond D. Douglas and Douglas P. Adams, Elements of Nomography, McGraw Hill, New York, 1947, p. 30; cited in David D. McFarland, “Addition and Subtraction With Slide Rules and Allied Instruments Part I, Journal of the Oughtred Society, Vol. 12, No. 2, Fall 2003, p. 34. (↑)
61 Robertson, A Treatise of Mathematical Instruments, 1775. (↑)
62 eg for brewing: John Palmer, How to Brew, Chapter 15, viewed 16 July 2012; or to estimate boiling temperatures at various temperatures Pressure Temperature Nomograph, viewed 16 July 2012 (↑)
63 Robert Wilson, “Who invented the calculus? - and other 17th century topics”, Gresham Lecture, Gresham College, Cambridge, 16 November 2005. http://www.gresham.ac.uk/sites/default/files/calculus1.pdf, viewed 2 May 2012. (↑)
64 ibid (↑)
65 W.R. Laird and S. Roux (eds.), Mechanics and Natural Philosophy before the Scientific Revolution, Springer, US, 2008, p. 259. (↑)
66 Vitruvius, De architectura (“Ten Books on Architecture (trs Morris Hickey Morgan), Book X, Chapter IX. ^ viewed 18 July 2012 (↑)
67 Flavio Russo, Cesare Rossi and Marco Ceccarelli, “Devices for Distance and Time Measurement at the Time of the Roman Empire”, in Hong-Sen Yan and Marco Ceccarelli (eds.), International Symposium on History of Machines and Mechanisms, Proceedings of HMM 2008, Springer, US, 2009, pp. 102–6. (↑)
68 ibid p. 260. (↑)
69 P. Ioanne Ciermans, Mat Professsore, Annus Positionum Mathematicarum Quas defendit ac demonstrauit, Soctis Jesu,1641, Novembris Hebdomas, Prima Problemata. This section reads, inter alia: “PROBLEMATA Multiplicandi, diuidendique numeros, compendia quaesiuere multi, & inuenere, sed plus fere, sua instrumenta ut concinnent, absumunt temporis, quam communi modo numeros permiscendi exigeret labor. Nos itaque ita paruam rotulis instruimus machinam, ut indiculis tantum nonnihil contortis opus sit, ut propositu quemcunq; per datum numerum, multiplicemus, partiamurque, idque sine ulla quidem erroris suspicione, tam certo ordine movenutur haec omnia, numerumque multiplicatum, aut divisum exhibit.” (↑)
70 “History of Computers and Computing, Mechanical calculators, Pioneers, Wilhelm Schickard”, http://history-computer.com/MechanicalCalculators/Pioneers/Schickard.html viewed 7 May 2012 (↑)
71 Benjamin Nill, “WWW-basierte interaktive Visualisierung der Rechenmaschine Wilhelm Schickards durch ein Java 3D-Applet”, Studienarbeit von Benjamin Nill, Betreuer: Dr. Bernhard Eberhardt, Frank Hanisch, Wilhelm-Schickard-Institut für Informatik Graphisch-Interaktive Systeme (GRIS), Universität Tübingen, September 1999 http://www.gris.uni-tuebingen.de/edu/projects/schickard/studw_1.pdf viewed 21 June 2012. (↑)
72 Max Caspar, Kepler, translated and edited by C. Doris Hellman, Dover Publications, London, 1993, p. 48. (↑)
73 ibid p. 46. (↑)
74 ibid p. 49; “History of Computers and Computing, Mechanical calculators, Pioneers, Wilhelm Schickard” (↑)
75 For these letters see Schickard’s complete correspondence in Friedrich Seek (ed)., Wilhelm Schickard Briefwechsel, Frommann-Holzboog, Stuttgart-Bad Cannstatt, 2002, i:135 and 141–142. (↑)
76 “…Arithmeticum organum alias delineabo accuratius, nunc et festinate hoc have”, which translates as “…I will describe the computer more precisely some other time, now I don’t have enough time” - see also http://meta-studies.net/pmwiki/pmwiki.php?n=Site.KeplersLetters (↑)
77 Max Caspar, in his research into the Kepler archives in the Pulkovo Observatory (near St Petersburg, Russia) found a slip of paper in Kepler’s Rudolphine Tables which appeared to have been used as a book mark, but containing Schickard’s original drawings for his “Calculating Clock” in a letter to Kepler. Somewhat after Dr Franz Hammer whilst carrying out research in the Württembergischen Landesbibliothek (Stuttgart, Germany) found a sketch of the machine (the second sketch reproduced here) together with notes to artisans on building the machine. (↑)
78 found by Dr Hamer in the Württembergischen Landesbibliothek (↑)
79 This fully working replica (albeit with the limitations to the carry mechanism as described below) was constructed through a collaboration of three European public museums and one private museum, under the coordination of Reinhold Rehbein. It was purchased for collection Calculant in 2011. (↑)
80 This particular calculation is explained in more detail in Friedrich W. Kisterman, “How to use the Schickard calculator”, IEEE Annals of the History of Computing, January–March 2001, pp. 80–85. (↑)
81 Henry Hallam, Introduction to the Literature of Europe in the Fifteenth, Sixteenth, and Seventeenth Centuries, Harper & Brothers, 1842, p. 406. (↑)
82 Michael Williams, A History of Computing Technology, p. 107. (↑)
83 Mark Napier, Memoirs of John Napier pp. 416, 432. (↑)
84 O’Connor andRobertson, “John Napier”, http://www-history.mcs.st-andrews.ac.uk/Biographies/Napier.html. (↑)
85 Mark Napier, Memoirs of John Napier, p. 421. (↑)
86 Quoted in Herman Goldstine, The Computer from Pascal to Von Neuman , Princeton University Press, Princeton, p. 6. (↑)
87 Translation as quoted in Michael Williams, A History of Computing Technology, 2nd Edition, IEEE Computer Society and The Institute of Electrical and Electronics Engineers, Inc., USA, 1997, pp. 120–1. (↑)
88 ibid (↑)
89 Michael Williams, History of Computing Technology, p. 125. (↑)
90 Jean-François Gauvin , Habits of Knowledge: Artisans, Savants and Mechanical Devices in Seventeenth-Century French Natural Philosophy, The Department of the History of Science, in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the subject of History of Science, Harvard University, Cambridge, Mass., USA, November 2008, pp. 229–45 (↑)
91 Crafted by Jan Meyer, Germany, from brass and mahogany, 2011 (↑)
92 Jean Mesnard (ed.), “Pascal, Entretien avec M. de Sacy sur Epictète et Montaigne”, in Pascal, Oeuvres complètes, 4 vols., Desclée de Brouwer, Paris, 1964–1992, pp. 124–157 (translation from Jean Khalfa, “Pascal’s theory of knowledge,” in Nicholas Hammond (ed.), The Cambridge companion to Pascal, Cambridge University Press, Cambridge, 2003, p. 123. (↑)
93 Denis Diderot and Jean le Rond d'Alembert, Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, Société de Gens de lettres, 1st edition, vol. 22, 1759. (↑)
94 From http://en.wikipedia.org/wiki/File:Lantern_gear_-_Turret_clock_from_1608.jpg viewed 1 June 2013. (↑)
95 Blaise Pascal, "Lettre dédicatoire à Monseigneur le Chancelier sur le sujet de la Machine nouvellement inventée par le sieur B.P. pour faire toutes sortes d'opérations d'arithmétique par un mouvement réglé sans plume ni jetons, Avec un avis nécessaire à ceux qui auront curiosité de voir ladite Machine et s'en servir". Suivi du Privilège du Roy., 1645, http://www.bibnum.education.fr/calculinformatique/calcul/la-pascaline-la-«%C2%A0machine-qui-relève-du-défaut-de-la-mémoire%C2%A0» viewed 19 July 2012 (↑)
96 Pascal, ibid, final page. (↑)
97 See http://meta-studies.net/pmwiki/pmwiki.php?n=Site.SchicardvsPascal (↑)
98 Francis Bacon, The New Organum, 1620, final paragraph, text reprinted at http://www.constitution.org/bacon/nov_org.htm, viewed 21 Jun 2013. (↑)
99 see for example, Bury, The Idea of Progress. (↑)
100 For a modern engineering description of the remontoire ascent-descent cycle see Branislav Popkonstantinović, Ljubomir Miladinović, Miodrag Stoimenov, Dragan Petrović, Gordana Ostojić, Stevan Stankovski , “Design, Modelling and Motion Simulation of the Remontoire Mechanism”, Transactions of FAMENA, XXXV-2, 2011, pp. 79–94. (↑)
101 Gauvin , Habits of Knowledge (↑)
102 Jean-François Gauvin, "Instruments of Knowledge," in the Oxford Handbook of 17th-Century Philosophy, ed. by Desmond Clarke and Catherine Wilson, Oxford University Press, Oxford, UK, 2011, pp, 315–337. (↑)
103 A particularly seventeenth century development, positioning those of standing beyond those in the nobility, as still somehow aligned to that status by demonstrating an ideal style of human qualities where the person combined a measured quality of heart and mind with, amongst other things, a broad grasp of current intellectual concerns, integrity, and the cultured politeness of courtiers. (↑)
104 From Les collections du musée Henri Lecoq, volume V, “Les Machines Arithmétiques De Blaise Pascal”, the cost of a machine was about 100 livres at a time that the average wage was about one livre per day. http://calmeca.free.fr/calculmecanique_php/rubriques/Fichiers_Blaise_Pascal/Fichiers_historique/Pascaline_histoire.php?lang=eng, viewed 25 June 2013]] (↑)
105 Pascal, introduction to “Avis nécessaire” in Lettre dédicatoire à Monseigneur le Chancelier, p. 9. (↑)
106 Balthazaar Gerbier to Samuel Hartlib, 4 October 1648, in S. Hartlib, The Hartlib Papers: A Complete Text and Image Database of the Papers of Samuel Hartlib (c.1600–1662), ed. J. Crawford, Ann Arbor, Michigan, 1995, ephemerides (1655) part 1, cited in cited in Ratcliff, “Samuel Morland and his calculating machines”, p. 174. (↑)
107 Gauvin, Habits of Knowledge, p. 117. (↑)
108 ibid, p. 230. (↑)
109 see for example, Rechenmaschinen-illustrated (↑)
110 James Orchard Halliwell-Phillipps, A brief account of the life, writings, and inventions of Sir Samuel Morland: master of mechanics to Charles the Second, E. Johnson, Cambridge, 1838, p. 7. (↑)
111 ibid, p. 8. (↑)
112 Autobiographical Letter to Dr. Thomas Tenison, 1689, reprinted in H.W.Dickinson, Sir Samuel Morland: Diplomat and Inventor 1625–1695, Cambridge,1970. (↑)
113 J. R. Ratcliff, “Samuel Morland and his calculating machines c.1666: the early career of a courtier–inventor in Restoration London”, British Journal for the History of Science, Vol 40, number 2, June 2007, pp. 159–179; and Halliwell-Phillipps, A brief account of the life, writings, and inventions of Sir Samuel Morland p. 9. (↑)
114 Diana H. Hook and Jeremy M. Norman, Origins of Cyberspace Novato, California, 2002, p. 111 (↑)
115 Michael R. Williams, A History of Computing Technology, p. 137. (↑)
116 Ratcliff, “Samuel Morland and his calculating machines”, p. 168. (↑)
117 J. Moore, A Mathematical Compendium, London, 1681, p. 21. (↑)
118 Justel to Oldenburg, 27 June 1668 and 15 July 1668, in Hall and Hall, cited in Ratcliff, “Samuel Morland and his calculating machines”, p. 175. (↑)
119 Robert Hooke, diary, 31 January 1672/3, cited in Dickinson, Sir Samuel Morland (↑)
120 Encyclopaedia Britannica, http://www.britannica.com/EBchecked/topic/335266/Gottfried-Wilhelm-Leibniz/4131/The-Hanoverian-period, viewed 25 June 2013. (↑)
121 Williams, History of Computing, p. 136. (↑)
122 Gottfried Wilhelm von Leibniz, School of Mathematics and Statistics University of St Andrews, Scotland, October 1998, http://www-history.mcs.st-andrews.ac.uk/Biographies/Leibniz.html, viewed 25 June 2013. (↑)
123 From François Babillot at calmeca.free.fr/calculmecanique_php/rubriques/Fichiers_Les_Techniques/techniques_entraineurs.php?lang=fra, viewed 30 June 2013 (↑)
« Part 1 Origins | | Part 3 The Late Modern Period (1800-) »
Pages linked to this page
 This work by Jim Falk is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License Click on the logo to the left to see the terms on which you can use it.
This work by Jim Falk is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License Click on the logo to the left to see the terms on which you can use it.