« Introduction | | Part 2 The Modern Era »
Part 1. Origins
| Mini: PHP-GD image library not found. Exiting. | Mini: PHP-GD image library not found. Exiting. | Mini: PHP-GD image library not found. Exiting. | Mini: PHP-GD image library not found. Exiting. | Mini: PHP-GD image library not found. Exiting. |
On this page… (hide)
- 1. Counting, numbers and counting technologies - did one come first?
- 2. Numerals, counting and counting devices - a symbiotic relationship
- 3. Calculating technologies, and the evolution of mathematics
- 3.1 Pragmatic mathematics - Mesopotanian, Egyptian, Chinese and Indian foundations
- 3.2 Greece - philosopher and practitioner - a “two track” mathematics.
- 3.3 Roman parallels
- 3.4 Measuring, timing, calculating and astronomical prediction.
- 3.5 Building on multiple pasts - the “Arabic hegemony”
- 3.6 Dimensions of development
1. Counting, numbers and counting technologies - did one come first?
Any account of the history of arithmetic (and it’s big brother, mathematics) is to an extent thwarted by the fact that mathematical capacity, and almost certainly mathematical thinking, extend back before the time of recorded human history. There is by now growing evidence that some mathematical capacity is shared not only by humans but also by a range of animals, including monkeys and some fish and birds.1 In short, some of our mathematical reasoning probably reflects an evolved endowment of the human brain. For that reason the axiom that equals subtracted from equals leaves equals (one of Euklid’s “common opinions”) is perhaps something we “know” rather than “arrive at”.
While clearly there are capabilities in the human brain which enable quantity to be assessed, we need to resist the temptation to believe that particular mathematical capacities are ‘hard wired’ through evolution (and then make some retrospective argument about how that would have been good for survival). Some underlying capacities no doubt are innate, but determining which of them are is a difficult process. Indeed, a range of new highly revealing imaging technology supports a now widely held view within the field of neurophysiology that brains, including the human brain, are remarkably “plastic”. That is they are self-organising, with the growth of neurones and connections between them being promoted by what we think about, and what we do. This capability has no doubt enabled creatures with brains, such as ourselves, to adapt more effectively to changes in our environment. This same capacity will to some extent allow the brain to “rewire” itself in a way that increases its capacity to reason mathematically. That will be shaped in part by the incentives in a society at a particular time for its members to be able to use mathematics.
But this rewiring of our brains is in turn directed in part by the way we mould our context. That is shaped not the least by the technologies we create to assist us. For example, in the first half of the last century there was increasing social demand to be able to do mental arithmetic. So quite possibly we developed within our brains enhanced capacities to do that. With the advent of personal computing machines that capacity is less called upon. As has been pointed out forcefully more generally about computers and the internet,2 from this point of view, calculators, as we create and use them, may be reshaping our brains and their capacities to do certain forms of mathematical and associated reasoning.
It may be useful to think of the emergence of counting in an unusual way (at least in terms of the literature). First we may recall that in the approach to ‘artificial intelligence’ in which networks are set up using computers to mimic the neurological networks in the brain, these prove remarkably effective in pattern recognition.3 The distinction between counting and pattern recognition can be fine indeed. For example, in one of numerous experiments carried out with animals, chicks when imprinted with five objects as constituting their ‘mother’ then searched for her when two of the objects were removed.4 Similarly, recently it was reported that a neural network which had not been programmed with the concept of number was able to develop a capacity to identify patterns which had more dots.5 Said the leader of the research, Marco Zorzi (University of Padua) “It answers the question of how numerosity emerges without teaching anything about numbers in the first place.”6
Another clue to the long-standing nature of the required evolutionary endowments is found with experiments with baboons which were able to be taught not only to discriminate between four letter English words and nonsense combinations but also to achieve increased capacity to guess whether a word they had not seen before was an English word.7 This shows the surprisingly sophisticated and relevant capacities of pattern recognition likely to have been possessed even by the human species’ evolutionary ancestors.
It is possible therefore that the act of counting is one where an evolutionarily endowed physical capacity for pattern recognition is complemented by the capacity to manipulate objects (whether fingers, marks on bones, or counters) thus constructing abstract formulations of the pattern in relation to observed patterns. From this the invention of words to associate with the abstraction is but one additional step, and symbols as shorthand for those words, another. This raises the interesting question of whether the usual assumption that calculators were invented to assist counting should be reversed, with the possibility that the (very rudimentary) calculator was a necessary step towards developing counting.
One technological practice which is believed to have existed as long ago as the Upper Paleolithic period (40,000–10,000 years ago) in the region of Lower Austria (Moravia) and South Poland, is weaving. In excavations (dated as early as 35 thousand years ago) imprints of textiles have been found on the surface of some ceramic fragments.8 Weaving certainly involves a capacity for pattern recognition, and perhaps some concept of tracking the quantity of successive threads. Perhaps this is an early indication of the building blocks for mathematical thinking already in play.
There is by now evidence from both anthropological and psychological research relating both to the oral presence of numbers in different societies and the presence of written words or symbols for them. Indeed this has led to the emerging field of ethnomathematics. However, the conclusions are not clear cut. We may simply all share some basic capacity to do counting and mathematical thinking. But what is innate in this way is hard to pin down. In any case, whether and how that capacity is taken up and developed will depend on the cultural and historical circumstances and needs of a culture. Indeed, whilst there are differences in what we recognise as mathematical cognitive abilities in different societies it seems that these differences cannot be taken to “imply necessary distinctions between right/wrong, simple/complex or primitive/evolved.”9
There is plenty of archeological evidence that the capacity to count is very ancient. Boyer and Merzbach suggest that it came about first through recognition of sameness and difference, and then over time the recognition that collections of things with sameness can be given a short description which we now call number. They suggest this process was probably very gradual and may have evolved very early in human development, perhaps some 300,000 years ago - about the same time as the first known use of fire.10 However they are also quick to note that whilst we may make conjectures about the origins of the concept of counting, since counting emerged prior to the earliest civilisations and certainly before written records, “to categorically identify a specific origin in space or time, is to mistake conjecture for history.”11
Nevertheless, there is evidence that the idea of associating things to be counted with a set of abstract counters is long standing. A Baboon bone dated from 35,000 years ago (amongst others of similarly great age) has been found with what are believed to be tally marks scribed on it.12) Another more recent bone, from about 25,000 years ago (see below) found in the village of Ishango at one of the farthest reaches of the Nile, has a much more complex set of notches which may be calculating tables, but is probably a crude lunar calendar.13

Ishango Bone - a small piece of Baboon fibula marked with 3 rows of well defined tally-mark notches ~25,000 BC. Reproduced courtesy of the the Smithsonian Institution Museum of Natural History (under its terms of use).
The prevalence of five and ten based counting systems in the most ancient surviving records suggests that the fingers also have long been used as a handy, although not universal, set of counters. (The Kewa people of Papua New Guinea are reported to count from 1 to 68 on different parts of their bodies.)14 Australian Aboriginal and Islander groups, contrary to earlier reports that they had limited number systems, have been shown to be able to count with facility, not necessarily by reciting the words for numbers, but by subitizing - relating the numerosity of a set of objects to grouped ‘hands’ of fives.15 The earliest counting, it has been suggested, may likely have been with pebbles which were conveniently at hand. But even though this seems credible, their use in this way may prove illusive to discovery through contemporary archeology.16
There may be a temptation to suggest that the earliest surviving instance or record of a calculator constitutes the moment that the technology of calculation first emerged. But as the above suggests, this is a crass simplification. Even beyond fingers and stones the earliest approaches may have been made using scratches in the dust, or fragile organic materials (such as leaves or pieces of grass), which except perhaps in very dry graves, would be unlikely to stay the distance. Thus for example we do not know the many possible ways early devices such as the knotted string khipu17 of the Incas was used. We do know that this device, always composed of many strands of knotted strings, but with great diversity in its use, not only represented a decimal, double entry accounting system, but also was used in functions of state. They ranged from recording outcomes of the national census as carried out district by district, and then compiled nationally, to the calculation of tributes, culturally significant astronomical events, and much more.18 A surviving example is shown below.19

Inca Khipu - made of 322 strands and said to be from Nosca, Peru. Museum of World Cultures, Göteborg, Sweden (photo courtesy of Gary Urton)
The earliest surviving tokens recognised by archaeologists as being for counting and (primitive) accounting can be found from 8,000 BC in the remains of Neolithic settlements. This was a time of early deployment of agricultural practices, in what is now Syria and Iran. Success in agriculture could be enhanced by record keeping as well as exchange. This was now appropriate since settlement enabled an increasingly sophisticated division of labour to emerge. Over the next five thousand years (to 3,100 BC) these artifacts can be seen to evolve to tokens (essentially pebbles fashioned from clay but with different shapes to connote different things, such as a disk representing one animal, or a cone representing a quantity of grain). Examples are shown below.20

Complex Tokens - from Susa, present day Iran, ~3300 BC. Below from left to right: one sheep, one unit of textile, 1 unit of honey, one jar of oil. Above from left to right: one ewe, ?, one ingot of metal. The objects are kept at the Musée du Louvre, département des Antiquités Orientales, Paris, France. Courtesy Denise Schmandt-Besserat.
These tokens were in time enclosed in clay envelopes holding tokens of particular transactions strung together on strings. Envelopes, however, hid the enclosed tokens and so envelopes emerged bearing images of the contained tokens impressed on their surfaces. Later clay envelopes can be found with signs not merely impressed upon them but also scribed into them.21 For an example see below.

Impressed envelope- with its token content from Susa, present day Iran, ~3300 BC. The large and small cones are units of grain. Each of the lenticular disks stand for 10 sheep. The objects are kept at the Musée du Louvre, département des Antiquités Orientales, Paris, France. Courtesy Denise Schmandt-Besserat.
As Schmandt-Besserat points out in her important, although not uncontested account,22 “The substitution of signs for tokens was no less than the invention of writing.”23 This supports the observation, made by several authors,24 but developed in considerable detail by Schmandt-Besserat that these inscriptions not only preceded the appearance of the first known written alphabet (cuneiform) but also appear to prefigure it. This lays a basis for the intriguing proposition that rather than writing being the basis for mathematics, the primitive technologies of calculating (and the mathematics that underlies it) may have not only preceded but formed the basis for the development of the first written scripts upon which has been built the technology of writing.
The Sumerian civilisation, as already mentioned, was the source of cuneiform script, the earliest known alphabetic writing system. In the period prior to 3,500 BC in the fertile plain of Mesopotamia between the Tigris and Euphrates rivers an advanced system of settlements, agriculture, irrigation and social organisation provided an equally fertile environment for the invention and widespread use of cuneiform. The number system developed within this script was based on powers of sixty rather than powers of ten as in contemporary systems. Even so, these ‘sexagesimal’ numbers25 were constructed with patterns corresponding to the numbers from 1 to 10. During the period of Akkadian rule, which lasted to 2100 BC, the abacus entered Sumerian life creating a further extension to the capacity to form basic arithmetic operations. The Babylonian civilisation replaced that of the Sumerians around 2000 BC.
Whilst the Babylonian civilisation replaced that of the Sumerians there was continuity in the specialisation of roles in the community, the reliance on trade, and thus a value on numerical script. The object shown below is an Old Babylonian tag receipt for animal carcasses including 1 ewe and 1 ram, from between 1934–1924 BC, and is covered in the administrative script of the time - numbers, alphabetic characters, and the imprints of official seals. Originally on a string the seal indicates the receiving party was important, since the seal legend was dedicated to a king, perhaps of Isin.26
 |  |  |
Babylonian tag receipt for animal carcasses including 1 ewe and 1 ram, 1934–1924 BC: (collection Calculant)
Large numbers of cuneiform tablets found in archaeological digs reveal that by now a mathematical system, recognisable to modern sensibilities, had emerged. This went hand in hand with the development of an organised urbanised agricultural society achieving significant construction (especially of canals). The day was divided into 24 hours, the hour into 60 minutes, the minutes into 60 seconds, and the circle was divided into 360 degrees. All of this sexagessimal flavour persists to the present. The tablets (for example, see below27) showed now the construction of reference tables to aid calculation including squares of numbers, tables of reciprocals to aid division, and more.

Babylonian scribal tablet showing list of reciprocals ~1800 BC. MS 3874 Friberg, A Remarkable Collection (2007), 69. Courtesy of Jöran Friberg.28
A basic form of algebra had also been developed, with equations and solutions, including solutions to quadratic equations that arose in the course of engineering of canals and other structures.29 Schools were also established so that the knowledge required to read and write cuneiform, and perform mathematical operations using it, could be transmitted.30 In this sense, now recognisably analogous to modern writing and media, the cuneiform tablets, combined with a social order which both needed them, and trained in their use, more than 3,000 years ago had emerged as a socially powerful mathematical and scribal technology.
The idea of numerals to represent numbers diffused and developed over following centuries emerging in different representations in different places. True to the importance of the human hand, most of these systems privileged the number 5 and 10, with 10 emerging as the most common “base” the powers of which shaped the meaning of successive positions in a string of numerals. Two different innovations should be distinguished here. The first is to develop numerals corresponding with successive quantities. The second is to develop a “place value” system of writing down numerals. In such a system the place a numeral occupies indicates that the corresponding number is multiplied by a power (determined by the placing of the numeral) of the base . (For example, in modern script, whose base is 10, and whose places from the right indicate “units”, “tens”, “hundreds”, etc, the number 123 represents 1×10×10 + 2×10 + 1×1).
It is unwise to assume that the history of counting, numbers, and indeed script has a single line of development. Stephen Chrisomalis cautions us, it is highly probable that “the modern place value numerical notation, or something quite like it, developed at least five times idependently” - in: Mesopotania (as already mentioned ~2100 BC), China in ~14–1300 BC, India in ~500 AD, and the Andes in or before 1300 AD, with the explanation that it is not as big a cognitive leap to develop such a system when it proves useful as is often suggested.31 To put it another way, some combination of our biologically endowed cognitive capacities and underlying evolved cultural building blocks may be conducive to assembling quantities in this way.
Some 100 different scripts have been identified which have emerged over the last five millennia.32 Of these numeric scripts, however, the earliest dated are the Proto-Cuniform (already discussed) and the ancient Egyptian. The ancient Egyptians developed a number system which was different in the base (this time 10 rather than 60 in cuneiform) and in the characters used. The ancient Egyptian system of hieroglyphic numerals, developed as early as 3250 BC,33 had characters for 1 and then the powers of 10 (10 - a vertical stroke, 100 - an inverted wicket, 1000 a snare, etc.) with the numbers from 1 to 9 simply shown as the corresponding repetition of the number 1. Thus for example, the number 12345 would appear as 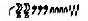 .34 However, after about a millennium of use of this system another “Hieratic” script was developed for use on Papyrus for routine use as opposed to the hieroglyphic script which was retained for carving in rock. The Hieratic numerals (shown in the table below) had by now taken what to modern eyes is the more efficient form of single symbol “ciphers” to represent each of the integers from 1 to 10 - the same concept which forms the basis for the modern numerals in use today.
.34 However, after about a millennium of use of this system another “Hieratic” script was developed for use on Papyrus for routine use as opposed to the hieroglyphic script which was retained for carving in rock. The Hieratic numerals (shown in the table below) had by now taken what to modern eyes is the more efficient form of single symbol “ciphers” to represent each of the integers from 1 to 10 - the same concept which forms the basis for the modern numerals in use today.
As shown below, other early representations similarly drew directly on patterns representing counters (or fingers). (Even the Roman system can be seen as counting to five on the one hand, reserving the thumb and forefinger for the V to represent five, and the X representing a V on each hand). The Egyptian Hieratic and then the Greek system replaced combination numerals with single characters, and finally, from the eighth century, the familiar symbols of the modern (Arabic-Indian) place-based system (complete with the numeral 0 to replace earlier spaces for “place holders” finally emerged.35
| Number System | Script36 | Base | ~ Century Introduced37 |
| Proto-Cuneiform |  | 60 | 3200 BC |
| Egyptian Hieroglyphic38 | 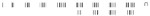 | 10 | 3200 BC |
| Egyptian Hieratic39 | 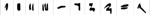 | 10 | 2600 BC |
| Greek | 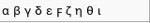 | 10 | 575 BC |
| Roman |  | 10 | 500 BC |
| Chinese Rod |  | 10 | 300 BC |
| Indian40 C8 AD | 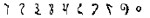 | 10 | 700 AD |
| Arabic41 C11 AD | 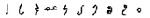 | 10 | 1000 AD |
| European42 (Arabic-Indian) C15 AD | 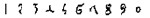 | 10 | 1400 AD |
| Modern (Arabic-Indian) C16 AD43 | 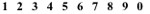 | 10 | 1549 AD |
2. Numerals, counting and counting devices - a symbiotic relationship
It is fairly easy to see how additional counting devices might evolve from the earlier primitive counting technologies. Most obviously marks, pebbles and tokens, and then grouped tokens, some of them strung like beads, lead fairly naturally to more efficiently arranged arrays of counters or special purpose rods, whether laid out on a backing, or strung along the lines of a primitive weaving frame.
Early devices include the development of knotted ropes used for both measurement and arithmetic operations. For example, two knotted ropes end on end may give the addition of two numbers. A knotted rope whose ends are brought together will provide a measure of half the original number, and so on. Further knotted ropes may be used to develop geometric relationships (for example, a 3–4−5 triangle can be used to set a right angle).44 Knotted ropes (see below45) were used (by “rope stretchers”) for measurement in ancient Egypt (and perhaps mathematical operations) - see below. Use of knotted ropes in ancient China is referred to wistfully by philosopher Lao-tze in the sixth century BC when he asks “Let the people return to the knotted cords and use them.”46

Rope stretchers - measuring the land for agriculture. Picture in the Tomb Chapel of Menna, Luxor (Thebes) ~1200 BC. Photo courtesy of the Musée canadien des civilisations
The Chinese are known to have moved from knotted ropes to a system of counting rods (see below)47, becoming very proficient in their use. Perhaps the earliest written account of the use of these comes from the Han Shu records of the Han Dynasty written by Pan Ku in 80 AD who relates that the ancient Chinese used sets of 270 rods to perform arithmetic calculations.48.

Metal counting rods - Western Han Dynasty, unearthed in Xi’an of Shaanxi Province ~0–200 BC
The rod numerals in the table of numerals shown earlier (and described by philsopher Ts’ai Ch’en (1167–1230 AD) give some indication of how these counting rods might have been used. Sun-tsu in the Third Century AD writes that the units should be vertical, the tens horizontal, the hundreds vertical and so on, and that single rod may suffice for 5. The results of a multiplication of 247 x 736 is given in this system by Yang Houei in about 1276. Such rods, made of bamboo, were known to have been in use in Japan by the seventh century AD, and were later replaced by more stylised “sangi pieces” - square prisms about 7 mm thick and 5 cm long and reasonably extensive records of calculations using chess board like “swan-pan” or “sangi boards” survive from the seventeenth century (see below49 ). Similarly, rods, made of bamboo and numbering 150 in a set, are still used in Korea.50

Swan-pan board - being used for calculation
The above innovations can be seen to fairly easily give rise to the emergence of different forms of counting machines. Of these the most well known surviving example in its multiple guises is the abacus. The invention of the abacus is attributed by some to the Akkadians who invaded the Sumerian civilisation around 2300 BC.51
However, what is to be taken to constitute an abacus has fuzzy boundaries. Arguably it has taken different forms as it emerged in different places at different times.52 Between pebbles on the ground and the abacus can be taken to lie counting rods (as developed by the ancient Chinese), and counting boards with scribed or otherwise arranged positions for counters. The word “abacus” is said to derive from the Semitic word abaq for dust, perhaps indicating that it developed from a sand tray used for counting. Latin (abakos) and Greek (αβαξ) versions of the word followed.53 There is reference by the ancient Greek historian Herodotus in the fifth century BC to hand movements where the Egyptians move from right to left in counting, whilst the Greeks move left to right, suggesting perhaps the operation of some counting frame or board. There is what appears to be a surviving marble counting board dated at around the fourth century BC in the National Museum in Athens (see the Salamis Tablet, below).54
Archaelogical evidence exists of the Roman embodiment of the abacus. Forms of it range from a wax tablet for scribing, a metal plate with sliders (of which one of the two surviving examples is shown below), a grooved counting board, or simply a table on which counters could be moved.55
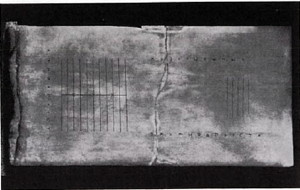 |  |
| Salamis Tablet ~300BC56 | Roman Abacus57 |
The abacus remains a highly efficient calculating device in widespread use across Asia and Africa. The emerging Arabic abacus was simply constructed of rows of wires bearing ten balls each, as still does the Russian abacus (“schoty”). The columns of the Chinese abacus (the “suan pan”) are divided into two sets of rows of beads, the upper ones each representing five on the lower section.

Chinese Abacus
(collection Calculant)
The Japanese abacus (“soroban”) has gone through a transition from the Chinese form (which arrived in Japan in about the 17th century AD), to a simplified form commencing about 1850 with only one bead in the upper, and five in the lower section, to a form nationally standardised in 1944 to only one bead in the upper, and four beads in the lower section for each column.58 In this sense it moved through various stages of development back to the configuration of the Roman abacus of two thousand years before.59
The symbiotic relationship between number systems and counting devices can be seen very clearly in the evolution of the abacus on the one hand, and the persistent use of Roman numerals right into the middle ages in Europe. The importance of counting technology to supplement such systems can be illustrated as follows:
This demonstrates the way in which counters, counting boards and rods, and eventually the abacus performed the essential duty of translation between pre-Indian numerals and the tasks of arithmetic. As Karl Menninger points out, this method was so effective that there was enormous reluctance to give up the old scripts even when the more efficient single symbol Indian-Arabic scripts were available. As he put it “The mutually complementary use of numerals and the counting board thus created a fully adequate and convenient tool for simple computation, which people were extremely reluctant to part with… Not only did Medieval Europe possess it (the modern place value notation) for many centuries, but it was throughly familiar to people even in antiquity - on the counting board.” But “It never occurred to anyone to try to take the step that the Indians had taken”.61
One could argue that the efficiency of the abacus is so great that there was no purpose in adopting the Indian script. For example, on 12 November 1946, in a competition overseen by the US Army Newspaper, between a selected expert practioner of the latest electric calculating machine and an expert soroban practioner the soroban practitioner defeated his opponent 4–1 in the tests of multiplication, division, addition and subtraction. Declared a report in the Nippon Times “Civilization, on the threshold of the atomic age, tottered Monday afternoon as the 2,000-year-old abacus beat the electric calculating machine in adding, subtracting, dividing and a problem including all three with multiplication thrown in, according to UP. Only in multiplication alone did the machine triumph…”62 63
However, the matter cannot be left there, for the use of counting boards and the abacus was also framed by the available media in which counting might be recorded. Metal and stone were used for writing in the early centuries in China. Clay was utilised by the ancient Sumerians. A much more tractable technology, papyrus, had been well used for a millenium in ancient Egypt but was unknown in ancient Greece before 700 BC. Parchment was invented around 400 BC. Paper came much later. It has been argued that the combined factors of cumbersome numerals, and difficult to use writing media, created a strong pressure to develop other technologies, such as the abacus, to complement them.64
Thus whilst the power of the abacus is indeed great - in highly trained hands - the social need for more widespread arithmetic capabilities in an ever more numerically ordered economcy, the cheap availability of paper, and the advent of printing and improved writing technology, made the capacity to calculate on the page, without any intervening calculating device, increasingly valuable. That could indeed be recognised as made much easier by an efficient positional decimal script. Thus the growing commercial pressure for wider arithmetic literacy in Europe was probably a factor in the adoption of the efficient Arabic-Indian script and abandonment of the abacus and counting board. (Much later, in the current period, this need for even wider basic mathematical literacy literacy would also be facilitated by cheap and freely available electronic calculators. The need for that, and battle to devise it, is a much later part of this story.)
To summarise, the development of systems of counting, technological modes of facilitating them, and particular social systems have co-evolved hand in hand. The process has often been quite slow and incremental. New ideas have not necessarily displaced old ones in practice for very long periods of time, if ever. And different evolutionary trajectories have developed in different social, economic and historical settings. But this insight is not restricted to the co-evolution of counting, numeration and supporting technologies. This incremental process of development has played out in different ancient societies not only in the business of arithmetic, but also in the development of broader mathematical concepts.
3. Calculating technologies, and the evolution of mathematics
The above has focussed on the evolution of counting and the technologies of that. Yet, as already suggested in the discussion above, there is a seamless overlap between counting, and the broader fields of arithmetic and mathematics. One observation which is suggested, not always spelt out in the literature, is that a mathematical idea or artifact which appears to have been “invented” in a single leap of inspiration will more likely have evolved very gradually. The appearance of sudden invention is not unlike the “missing link” between baboon and human which used to be considered a problem for the theory of evolution. Now sufficient of such links have been found to support the theory. But evidence for outmoded ideas are less available (which is one of the charms of calculators which do leave a more enduring evolutionary trail). Nevertheless, it is not hard to see how the use of counters (whether fingers, pebbles, rods, knots or beads) as proxies for specific things (sheep, tenants, corn bushels) leads beyond counting, seamlessly to addition and subtraction, and then to more sophisticated mathematical ideas.
There is an enormous literature on the history of mathematics. By now it covers many societies beyond the recognised roots of Western society in Greece, Rome and Egypt. There is of course a rich history of Arabic Islamic mathematics which is still only beginning to be recognised in the “West”, and beyond that the mathematical developments from societies ranging from the Inca, Indian, South American, to many surviving cultures of indigenous peoples. In this sense there is no single history of mathematics. More challengingly, there can be more than one “mathematics”, a word which itself derives from ancient Greece, but in contrast to current usage had a much broader meaning of “learning”.65
One seemingly quite general proposition which can reasonably be formulated from this literature is: pick any pre-modern society which has established sufficient record to be able to display its developments in the area of numerical and mathematical culture. There we will find practices of not only counting and basic arithmetic, but also invention and use of more advanced mathematical concepts. In each society, however, the particular sorts of emphases, consequent areas of discovery, and the way these are arrived at and formulated, may differ greatly. Further, the technologies used (whether, for example, use of diagrams, the abacus, or knots) will depend on the physical and social circumstances of the society. Here it is sufficient to illustrate this in the light of a few examples and make a number of observations about them.
3.1 Pragmatic mathematics - Mesopotanian, Egyptian, Chinese and Indian foundations
Mathematics has many expressions. But the evidence suggests, not surprisingly, that the beginnings were built by the people who needed to answer practical problems demanded by an increasingly sophisticated society. Examples include: how to build a regular shape (for example, a pyramid) and how many people would be needed, how much food would they need, how much tribute would be required to keep the administration in operation, what would be the crop production and how much could each person give? The people who needed this sort of mathematics were scribes and architects, builders, and those who supervised the payment of tributes. There were also others, who we will occasionally refer to here (not quite comfortably) as “artisans” (in the sense of skilled worker) or “practitioner” (in the sense of a pragmatic practitioner or practical mathematics). The beginnings of mathematics can be found in ancient Egypt and Mesopotania, derived pragmatically from experience and shaped and written down precisely by and for such practitioners (including officials).
Egypt
The role of environment on the form of mathematical development is famously illustrated by the case of ancient Egypt. Here the use of rope and rod measuring, and associated calculations and geometrical insights was essential to the calculation and arbitration of claims in relation to ownership of land after the regular Nile flooding. The Greek historian Heroditus after visiting Egypt claimed in about 450 BC that the origin of geometry (whose original meaning was “land measurement”) was Egypt.66 However, the idea that ancient Egypt had developed an elaborate discpline of geometry needs to be tempered by the character of mathematics which the Egyptians in fact created. As elsewhere this was shaped very much by the process of discovery itself, the culture, practices and challenges faced by the society, and as a consequence, the uses that society put mathematics to.
In Egypt, life was built around the fertile area of the Nile. Its periodic floods both laid down new soil and washed away salinity, but at the same time reshaped the land. There was a need for landholders to establish the boundaries of their land after this flooding and developing a means of proving those boundaries was an important motivation for the considerable advances in land measurement with knotted ropes and measuring sticks which can be found as far back as the records stretch. Over three thousand years of continuous civilisation gave rise to a complex society ruled through the sophisticated hierarchical dynastic governance of the Pharos. Accompanying that was the emergence of associated religious institutions (building legitimacy in part by a capacity for astronomical observation and prediction), complex economic taxation and trade relationships, and mining and fashioning of metal, and art, engineering and architecture (notably visible in the surviving pyramids, tombs and statues).
The extensive literature on ancient Egyptian mathematics needs to be read with the fact in mind that, in reality, the surviving written sources on the subject are very sparse. (In sum they are constituted from five papyri, a leather roll and two wooden tablets from 2055–1650 BC). Much of the historical attention focusses on the Rhind Papyrus, which appears to have been an instruction text for scribes, copied by scribe Ahmes in 1650–1550 BC from an older text from 1985–1795 BC.67 The papyrus presented a series of problems and worked solutions of the sort that scribes might have to deal with in their various roles, but always in the form of specific case examples, then developed with increasing difficulty.
Evidence from the above papyri is complemented from information which may be induced from surviving technological artifacts - structures, objects in tombs, and inscriptions on tomb walls. From this corpus it is possible to draw quite a wide range of conclusions.68 Here it is sufficient to note that the ancient Egyptians had developed a capacity to solve mathematical problems firmly rooted in the practical needs of the society. These needs included such things as calculating the area of land, the fraction of crops required in annual payment of dues to the state, the quality of products such as beer and bread (expressed as the “psw” or fraction of grain required to produce them), and quantities of ores and other ingredients to smelt metals. They knew about the practical measures required to measure out fields, and volumes of various shaped objects, and how to characterise a slope (for example of a pyramid by calculating the “sqd” - the distance, in number of palms, by which it deviated from the vertical in a vertical rise of one cubid). They found a workable approximation for the area of a circle, and thus a reasonable approximation to what we call pi.
Ancient Egyptian arithmetic was focussed on addition, with multiplication being carried out primarily through a process of repeated additions and doublings. They knew about fractions, but their attention was focussed primarily on reciprocals (in modern terms of the form {1/n} where n is an integer). Calculations which would result in other fractions (such as division or the extraction of square roots) were carried out using added sequences of these reciprocals. Tables of reciprocals were developed to assist such calculations. These insights were conveyed with the aid of simple diagrams (see the extract of the Rhind Papyrus below69), and mathematical ‘recipes’ rather like simple modern computer algorithms (especially in the most literal computer languages such as COBOL70), where the amounts of different quantities were first specified, and then the sequence of arithmetic steps that would be required to produce the required answer.71 The geometric problems were laid out in exactly the same way, and from this point of view, appeared more as applied arithmetic than what we now think of as geometry, with its constructive proofs which derive from the ancient Greeks, of which more later. There was a flavour of modern algebra in their introduction in these of ‘aha’ - a place-holder for a quantity that was to be determined in what were from a modern perspective linear equations, and their apparent understanding that multiplication is commutative (a x b = b x a).72 The papyrus is shown below.

Rhind Papyrus ~1650–1550 BC
The mathematics was thus of a very practical kind, with instruction being in terms always of concrete examples with specified amounts from which, presumably, the budding scribe would learn enough to then be able to do similar calculations in everyday working life. There has been found little of the emphasis on abstraction - the development of overarching proofs and theorems, abstract algebra, and the like which was certainly seen in the ancient Greek geometry and more generally mathematical reasoning. As Boyer and Merzbach put it “Even the once vaunted Egyptian geometry turns out to have been mainly a branch of applied arithmetic.”73 One reason for this lack of emphasis on abstraction may well be that the Egyptian civilisation was highly settled in its generously fertile and annually renewing Nile valley. There was not even a great need for attention to warfare, although battles did take place. But the society survived well on maintaining traditional practices and slow progression over its millenia of sustained existence. In short, it developed the mathematics it needed to meet what it saw as its challenges, and did not experience any intense incentive to develop more.74
This may be an explanation, but it is not necessarily the whole explanation. For example, the question arises for any society, who is doing the calculating, and for whom? Who is developing the methods, and why? The records we have are from scribes preparing other scribes for work in the various enterprises of the Egyptian society. This includes the work of going into the fields to estimate the annual dues, to arbitrate on behalf of the Pharonic order the disposition of land, to ensure that the work of metalurgy is carried out to meet hierarchical requirements, to prepare for religious rituals (for example the ritual measuring at the commencing of construction of a building), to estimate materials and labour required in major building projects, to account for progress, and to finally confirm the accuracy of work done.75 But much of the actual work would have been done on the ground, with answers to practical problems, whether it was how to built to a particular slope, or how to measure a large area, being developed by practioners. In this sense, the style of this mathematics and its representation may have been because it fitted a world in which mathematics was developed in practice, with practical answers being explained to others, learned and eventually inscribed on papyrus, perhaps after much development literally “in the field”. As will be discussed more later, this factor - of who the mathematics was for, and who was developing it, appears to be an important consideration in understanding the role and design in the development of new calculating technologies.
Mesopotania
The Sumerian civilisation, is often described as having displayed greater innovation than that by Egypt in its mathematical development. Whilst also situated in a fertile region, part of the explanation that can be offered is that the Sumerian civilisation experienced more disrupted circumstances, and in turn displayed greater inventive vigour. Whether or not that is the whole explanation it is certainly true, that to modern eyes with the vantage point of knowing the current form and state of mathematical knowledge, the Sumerian civilisation did make some striking advances. As in Egypt, the fertile Mesopotanian valley was the home to an imposingly organised civilisation under the governance of a strong highly centralised hierarchy. In maintaining and extending the stability and authority of its rule the rulers found it necessary to mount major irrigation works designed to irrigate and control flooding from the Tigris and Euphrates rivers. However, this land was the focus of invasions from many directions including, as already mentioned, that of the Akkadians, followed by a string of successive invasions and revolts.76 The mathematics was set within the technologies developed - the sexagessimal (base 60) number system, the cuneiform script, the use of clay as a scribal medium, the elaborate schooling system, and the calculational needs of this highly urbanised and organised society.
The successes of the Mesopotanian mathematics included the eventual development of a place holder symbol that allowed 22 to be clearly distinguished from 202 (in our script) and a realisation that fractions could be treated just like whole numbers (by similar means to our decimal numbers, albeit being written to base 60). Given this inventive direction the development of comprehensive look up tables for a variety of applications seems natural, and some survive.77 Utilising tables of outcomes, together with these insights into the capabilities of the number system provided a sufficient basis for greater facility to grow in multiplication and division. From this followed the development of some remarkable capacities which included the ability to extract square roots . For example, using a simple iterative method for working out square roots of numbers, and one of the surviving tablets gives the square root of 2 (in sexagessimal as 1 + 24 x 60−1 + 51 x 60−2 + 10×60−3) which is accurate to 5 of our decimal places. There was also a capacity to pose and answer questions which in our terms amount to not only linear, but quadratic and even cubic equations, and indeed answers to some simultaneous equations. There are even some tables of powers of numbers, which in principle enable the equivalent of logarithmic calculations to be completed. A range of remarkable other geometric and algebraic insights (see for example below78) have been recorded.79

Plimpton 322 Tablet ~1800 BC (held by Yale University) - bearing what is believed to be a table of numerical relationships between the sides of triangles and associated squares. It is Old Babylonian, and its layout and syntax indicate that it is from the ancient city of Larsa.80
All this is very striking, yet as with the Egyptians there is no evidence that the Sumerian civilisation or its later manifestations saw any need to prove their methods. Nor do we have much evidence of what role counting devices played in creating these numerical rules, even though the abacus itself is believed to have been introduced into the ancient Sumerian society.
China and India
China and India were also sites of ancient civilisations which as with Egypt, probably drew on developments in Sumeria but also were sufficiently isolated and long-standing to develop their own significant bodies of mathematical work. As with the Sumerian and Egyptian mathematics these were developed as solutions to practical problems, which were then elaborated also into solutions of teasing questions. Built on prior solutions to previous questions, new questions could then be developed. The answers however, were usually in the form of mathematical ‘recipes’.
In both cases the surviving historical evidence is not sufficiently robust to confidently answer the question of how far back this work extended. There is reason to place the first Chinese empire as stretching back to 2750 BC, although more conservative estimates assert a closer date of around 1000 BC. There is no more agreement on the dating of the oldest chinese mathematical work, the Chou Pei with estimates ranging from 1200 BC to 100 AD. Boyer in his imposing work opts for 300 BC.81 The Chou Pei and subsequent works reveal a mixture of “accurate and inaccurate, primitive and sophisticated results”.82 Certainly the Chinese mathematical development appears to have largely been of Chinese origin, although early lessons may well have be drawn from interchange with Mesopotania. The areas of triangles, rectangles and trapezoids are correctly calculated in the context of problems, and the area of the circle (with pi approximated by 3). Magic squares, the solutions to problems which would now be considered simultaneous linear equations, and the like are also solved. The development was not continuous, with developments disrupted by the occasional burning of books and other interruptions. By the fifth century Tsu Ch’ung-chih (450–501 AD) had performed the notable feat of establishing the value of pi to 6 decimal places. However, there remained sparse availability of written works even though printing was developed in China as early as the eleventh century AD.83 Two important treatises from 1299 AD by the great mathematician Chu Shih-chieh (1280–1303 AD) marked a peak in the development of Chinese algebra and revealed an understanding of how to approximately solve some quite sophisticated problems (for example, in modern terms, ones involving variables up to the 14th power - ie. x14).84
Similarly in India there appears to have been an old but sophisticated civilisation contemporaneous with the time of the construction of the Egyptian pyramids. Once more we see references to early arithmetic and geometric insights going back to 2000 BC, but there are no surviving documents to confirm this. Boyer considers it likely that India also had its “rope stretchers” to assist in the construction of temples and the like perhaps contemporaneous with the founding of the Roman Empire (from 753 BC). But any dating of this is speculative. Hindu mathematics has even greater discontinuity than that in China. The first known Indian mathematical text (by Aryabhata) is placed much later, traditionally about 476 AD (the time of the fall of the Western Roman Empire). There is subsequent evidence of significant geometric and algebraic insights, the calculation of pi (but less accurately than in China) and the development of astronomical measurements, all of which shows some influence from Greek mathematics (described below).85
As for improvements in calculation, the key Hindu invention of a system of numerals in which successive places stood for powers of ten has already been mentioned. This is explained in the text by the Hindu mathematician Aryabhata who in the sixth century noted that he carried out his calculations using a notation where “from place to place each is ten times the preceeding”. However, the earliest known inclusion of the numeral for zero (to represent an empty space) is from 876 AD.86 The Chinese are notable in this regard for their use of rods (black for things being added, and red representing things being taken away) and their subsequent representation of this with an equivalent set of numerals, the whole being controlled by use of horizontal rods to represent multiples of ten.
From what is available it does seem that the questions, and their answers, in all the civilisations mentioned above - Sumerian, Egyptian, Indian, and Chinese - were largely formed around practical problems (such as determining the dimensions and areas of regular bodies, and in particular triangles). In the course of this Pythagorean relationships between the lengths of sides were tabulated. These questions, intermediate answers, and methods for using these to give final answers were clearly systematically developed. The working of examples was greatly facilitated by developing appropriate scripts for writing that down. Technologies such as counting rods, sand trays, and later the abacus were used to complement that work. All of this was of practical importance, and at times also celebrated in high places. Significant texts appeared by leading mathematical scholars which summarised and taught what had been achieved. But none of this produced a body of mathematical knowledge in the systematic and abstract way that is both required and celebrated in modern mathematics. That is, the knowledge was not founded on methods of proof to establish its authority. The place where the desire, and methodology to do this emerged was in the mathematical writings of an elite group of mathematical philosophers in ancient Greece.
3.2 Greece - philosopher and practitioner - a “two track” mathematics.
There is more than one way of establishing the authority of a claimed truth. Religious pronouncements may base their claim to truth on the authority of a deity perhaps revealed through some particular humans. Then there is the authority of repeated observation. Repeated observation are the basis of common sense: that the sun will rise every day, that things released will fall, or that water heated enough will turn into steam. These observations may over time become so well accepted that they may be accepted as general laws.
Another form of authority, is that used to support the claims of truth in modern mathematics and the sciences. This is the authority which derives from clearly laid out logical deduction. Logical reasoning of course is used in all forms of argument. But the key to the way it is used in mathematics and science is that it is written down according to certain conventions. These allow the various steps of the argument to be seen very clearly, and if each is accepted as following logically from the previous, and the starting point is already accepted as being true, then the claim that the whole is true can be particularly convincing.
This highlights the difference between what surviving mathematical records reveal was done in ancient Egypt and Mesopotani (based on “recipes” for solving specific types of problems, usually based on an example), and the more abstract mathematical reasoning that emerged from ancient Greece and gave rise to our modern concepts of “proof”.
It is not necessary here to dwell for long on the expansive achievements of the ancient Greeks in the development of abstract geometry and mathematical reasoning. All this is described both in great detail, but also accessibly in summary elsewhere.87
There is a shadowy history of mathematics in ancient Greece. It begins with invaders from the north in the second millennium BC. They had no known capacities in literacy or numeracy. After that was the likelihood of trade and other interchanges with Egypt and Mesopotania. Later we have the sophisticated Greek literature, already evident by the first Olympic Games in 776 BC, and then the beginnings of the formal abstract mathematics for which the ancient Greeks have been so celebrated. That may be traced back to the illusive figures of Thales of Miletus (around 585 BC) and his use of geometry to solve practical problems, and Pythagoras of Samos (around 580–500 BC).88
The development of mathematics from these sources (and the oral mathematical knowledge which they may have formalised) flowered until the destruction of the Academy of Athens in 529 AD. That period saw the emergence of “schools” of mathematical philosophers including the magisterial Pythagorean School with its emphasis on proof (including, so it is believed, the proof of “Pythagoras’s Theorem”), Plato’s Academy in Athens (which became a centre of mathematics in the 4th century BC), and associated achievements including an iterative method used to determine the areas and volumes of complex curved and other objects. The achievements were famously brought together by Euclid in his Elements in the 3rd century BC in which the formalisation of what we now understand as ‘mathematical’ rigour and its use for “proof” was systematically displayed. Thereafter the “Golden Age” of Greek mathematics began to decline although there was nevertheless a series of significant analytic developments, especially in algebra.
It is not clear that there was any significant advance in Greek mathematics over the three hundred years from 150 BC to 150 AD. By then it was clear that the period of rapid growth of this field in Greece was at an end. It has been suggested that this decline was caused by an emerging emphasis on practical application. Others attribute the decline to difficulties now encountered in the approaches adopted. Others again attribute it to the waning power of Greece in relation to the military might of Rome.
There was a period from 250 to 450 AD when some innovative mathematicians made continuing contributions, notably Nichomachus of Gerasa (~100 AD) who wrote Introductio arithmeticae, Diophantus of Alexandria ~250 AD the author of a thirteen book treatise Arithmetica, and Pappus of Alexandria (~320 AD) who wrote his important Collection (Synagoge) of Greek mathematics. These various contributions are well described elsewhere.89 The mathematical outputs from Alexandria, which had become the centre of Greek mathematics at the time of Euklid (~300 AD), after a further 100 years, had come to an end.90 Over the following century, some further development occurred, for example, through Proclus of Alexandria (410–485 AD) who went to Athens and wrote an important Commentary on Book I of the Elements of Euklid. However, by ~500 AD not only Greek, but also as will be described, Roman mathematical development (and with them the entire production of systematic abstract mathematical development from the ancient world) had ceased.
The above is related to provide part of the context that of the development of calculating technology. Importantly, the abstract, and thereafter much celebrated invention of formally and systematically written abstract mathematical (and other applications) of reasoning, does not represent the only mathematics that was being performed. Indeed there was at least what Marcus Asper has styled “the two cultures of mathematics” in ancient Greece.91 To be more precise Asper stresses that recently “a consensus has emerged that Greek mathematics was heterogenous and that the famous mathematicians are only the tip of an iceberg that must have consisted of several coexisting and partly overlapping fields of mathematical practices.”92
This picture of a tapestry of mathematical practices being utilised by different participants in the society must be closer to the reality than two totally separated cultures. (The old joke comes to mind that ‘there are two classes of people: those who divide the world into two classes of people, and those who don’t’). Nevertheless, with that caveat it is useful to reflect on the fact that at least two practices were in play: the abstractions being developed by a relatively small philosophically inclined elite (what Asper calls “theoretical mathematics”), and the continuation of the practical mathematics in the style of useful recipes for practical purposes in everyday activities, which was the legacy of Mesopotania and Egypt, to name just two major centres (which will be referred to here as “artisanal” or “pragmatic” mathematics and which Asper refers to as “practical mathematics”93).
As Lloyd points out,94 this distinction between the abstract and pragmatically applied, can be found in Plato’s remarks on the quite different types of usefulness embodied in, on the one hand, meeting the needs of everyday life, and on the other of training the intellect. But the search for proof is the most striking feature of the abstract work of the Greek philosopher-mathematicians. And here we may see how the political culture of the time may have sharpened the desire for this. For the world of the Athenian free citizens was governed through the law courts and assemblies. In these, as Plato stresses, mere rhetorical skill could be sufficient to sway the participants, whatever the actual truth. But the claim that could be made for mathematical conclusions was that they were exact and proven. More generally, philosophy sought the same strength of truth and philosophers celebrated, developed, and recorded the types of mathematics which could be shown to meet this rigorous standard.
Whilst there are only glimpses of the more pragmatic mathematics we get a taste of it in Aristophanes play The Wasps from 422 BC:
Even in these couple of lines we seen enough to establish the gulf between the practical problems to be dealt with in day to day life, and the sophisticated highly abstract geometric reasoning of the classical Greek mathematicians. On the one hand, for example, is the highly abstract question of how to develop a pure geometrical method or system of harmonic ratios in order to understand musical harmony, or to prove a theorem about the volume of a geometric object in terms of its sides. This was the sort of question the tackling of which could be seen as a good intellectual preparation for the more important art of philosophical reasoning wherein the ‘really big questions’ could be tackled.97 On the other hand there was the practical question of how to keep track of resources from multiple sources. The methods for tackling this included the use of calculational aids (of which pebbles as counters were a frequently used technology). The former development in abstract mathematics was characteristically Greek. The latter, was common to all mathematically literate and complex societies (including those of ancient China, Mesopotania, Egypt and Greece).
What can we make of this? Asper argues that the abstract or theoretical “culture” of mathematics was developed by a small group of elite Greek citizens with an impetus that was partly aesthetic, partly a ‘game’ in which successful Athenian ‘gentlemen of means’ who could afford such pursuits would compete without the need to gain financial return.98 In place of wealth they gained prestige (and no doubt associated authority. This elite practice was focussed on communicating through a developing orthodox written form of discourse, general theorems about ideal geometric forms. The work emerged in the sixth to fifth century from practical roots. But the thrust was sharply against the ‘vulgarity’ of meeting practical needs. Indeed in its mode of presentation and areas of work it was directed to maintaining a sharp distinction between crude application versus the intellectual abstract search for proved knowledge which lay at its core.99
The less celebrated and less visible practical mathematics was more closely aligned to its anticedents in Egypt and Mesopotania, based around practical recipes for solving the multiple problems of daily life in a substantial and sophisticated urban society. Those problems were associated with the commercial, engineering, agricultural, religious, political and administrative challenges encountered in daily life. As Asper notes, this mathematics was derived from older traditions from the Near East, focussed on ‘real-life’problems, communicated actual procedures which by example illustrated more general approaches to encountered problems, and relied on written texts only in a secondary way if at all. Oral communication and guild training were the means of passing on the relevant approaches to practitioners in particular fields of work.100
Thus in the Greek story, the evolution of calculation merges into an evolution of mathematics, but divided across a spectrum marked by the pragmatic and practical at one end, and the theoretical and abstract at the other. Spread across that also are different forms of possessing and transmitting knowledge - from those of the philosophically oriented schools of abstract mathematics and their formalised presentations of written proofs (in a dispassionate and subjectless style still characteristic of modern scientific communication) to the specific oral and apprenticeship styles of transmission utilised by the practical problem-solving artisans.
The geometry of forms becomes the paradigm physical embodiment of the abstract end, whilst numbers, and simple calculational devices for manipulating them, most clearly the use of “pebbles” (whose origins are already shrouded at the dawn of humanity) is situated at the other. Pebble arithmetic, together with the means of measuring, weighing, sighting angles, and the like never appears in the theoretical accounts. But it has left sufficient shadow through sporadic references (such as in Aristophanes quoted earlier) to indicate that the use of pebbles as counters, often on a marked board, was widely used.101
Of course, quick use of pebbles on a special board is not an innate skill. Almost certainly its use was commissioned and practiced by a guild of skilled practitioners and many tricks could be developed to speed the process up, just as with the abacus in Modern Asian societies. The manipulation of pebbles, in patterns, and then stacked into volumes, is enough to provide a wide range of mathematical insights. So whilst the written works of the abstract mathematical game playing elite may never have mentioned it, an unknown number of insights no doubt translated from the more practical pursuits of the pragmatic world of calculation, with its pebble counting technologies and the associated group of professional pebble counting practitioners.102 In this sense the difference between the two tracks or cultures of mathematics was not just one of goals, nor of abstract versus pragmatic, but also of social class. An analogous social differentiation framed the use of calculating technology in ancient Rome.
3.3 Roman parallels
The Roman Republic (510–44 BC) gave rise to the Roman Empire which at its height stretched from England to the Persian Gulf, and ended with the fall of its Western half in 476 AD. Boethias (CE ~480–524) was perhaps the foremost mathematician produced by ancient Rome who also wrote a work on ethics, De consolatione philosophae, as he faced execution having fallen out of favour with the Emperor.103 His death effectively coincided with the end of mathematical development within the ancient Roman empire.
In fact, whilst the Roman society was a powerful military and organised system, its elite was not much attracted to the power of mathematical investigation, contributed little to what is known about mathematics, and gained much of its practical knowledge of mathematics from the civilisations Rome conquered and with which it traded, not the least from the ancient Greeks.104 The development of Roman numerals, and the importance of the use of the abacus in ancient Rome in manipulating them efficiently has already been discussed. Beyond this only one further aspect of the use of mathematics in Rome will be considered here as a useful illustration of a more general conclusion.
For even the limited synoptic history described already the relationship between the emergence of these mathematical systems and the needs and organisation of the societies is quite striking. In each case the evolution of counting and the technologies to facilitate that, has been shaped by, and helped shape the types of society which could be constructed. For the Egyptian and Sumerian civilisations which could settle in relatively climatically stable and fertile valleys, the consequent emergence of agricultural practices, and the correspondingly more settled agricultural societies led to the possibility and growth of a more complex urbanised social organisation. Work could emerge as a differentiated set of skilled and less skilled roles, with more diversified activities, including trade and barter. The regulation and arbitration of disputes related to this sort of activity developed along with some form of broader organisation of ruler and ruled, with accompanying trappings of allocation of land and other resources. Thus, the Old Babylonian laws (detailed in cuneiform tablets) laid down by King Hammurabi in the Code of Hammurabi from 1792–1750 BC lay down some 282 laws dealing with everything from the treatment of theft and adultery to the duties of workers, property rights, prices for services, obligations to neighbours,the graduated punishments” associated with “an eye for an eye”, the precept of “innocent until proved guilty” and an ancient form of minimum wage.105
Associated with the development of these more complex social orders there was the potential for the growth of powerful elites who could both deploy public resources for collective purposes (such as defence, irrigation and religious ritual), impose corresponding forms of taxation and record a census of the population and the extent to which citizens met their tax and other obligations. These increasingly complex forms of social organisation could lead to the desire and need for recording of roles, debts and assets, and more complex construction projects requiring estimation, measurement, and design.
Different social structures also support particular forms of calculation. Thus even with the legendarily cumbersome form of the Roman numerals, the society was now structured in a way in which a wealthy set of merchants and high officials began to rely on calculational devices and those who could operate them. It was not hard to access necessary labour. The picture below106 from a gravestone in the Museo Capitolino in Rome, shows a first century AD Roman merchant with his “calculator”107 - the person on the left who is using a hand abacus to tally amounts at the “dictation” of his master. A scribe to the right takes down the results.

Roman calculator(s) at work. ~0–100 AD
There is a subtle issue to be careful with in the above argument. It is generally an oversimplification to suggest that a social change led to a technological change or vice-versa. After all, it is certainly true that more complex forms of social organisation created the impetus to develop better forms of calculation, but it is also true that the invention of more sophisticated forms of calculation allowed these more complex forms of organisation to develop and flourish. What we can say is that the two - more complex society (in the sense of greater interdepenency and interaction across larger numbers of people and institutions), and corresponding governance systems (of a variety of types) - co-evolved with more sophisticated forms of mathematical capacity (which, as argued elsewhere, is part of a broader capacity for reflexivity).108
In particular, similarly to their Greek counterparts, the Roman capacity to meet the need to calculate in a complex hierarchical society was greatly facilitated by the use of counting boards, and in a more mature form, the abacus. As with the Greeks, it was not necessarily the user of the calculations who performed them. That task could be left to subordinates (whether free or slaves) who had gained the necessary skills by studying under a master of the art. Thus the abacus, as a calculational technology, together with the calculator who was skilled to use it, formed a symbiotic pair easing the processes of commerce, administration and engineering, in the developing Roman society.
3.4 Measuring, timing, calculating and astronomical prediction.
Whilst this discussion is focussed on calculation, the need for this is of course only one aspect of the developing needs of a complex society. As already mentioned, measurement has been equally crucial, and measurement and calculation form parts of a bigger whole. In all the evolving social settings mentioned so far, measurement has played an important role. This ranges from the work of the rope stretchers of Egypt (and Athens) to the early methodologies for measuring time (for example with sand and water flows,109 and the burning of graduated candles) in ancient Rome.
It is not surprising that the activities of the motions of the lights in the sky as they appeared in day and night would be the focus of much interest in many societies. The mysterious motions of celestial objects, the unatainable remoteness of the celestial sphere, clear influence of its activities with the seasons, and apparent correlations between celestial motions and weather, tides, lightening and thunder, and occasional destructive impacts on the earth pretty much guaranteed that these would be the subject of speculation and mystical interest. Many would claim special knowledge of these motions and their implications, ranging from the mystical claims of priests to those of astrologers. Their predictions and interpretations could be highly influential. Evidence of this can be found right through the archaeological record.
There was thus in most societies a relationship between religion, astrology and astronomical observation. In more sophisticated cultures this included also astronomical measurement. Many ancient structures and devices can be identified which served to measure astronomical events. They were used to predict future movements of the sun, moon, planets and stars, the seasons, and religiously significant events shaped by these. Many such devices have been found ranging from possible astronomical implications of the sarsen circular stone monument at Stonehenge110 erected in about 2200 BC to devices explicitly constructed to measure the angle subtended above the horizon by a star.
Astrology in particular is a central theme, based of course around different conventions for describing celestial configurations and events and different interpretations. Given no better explanation it was a reasonable presumption that the movements in the sky followed the dictates of gods, and thus could be a guide to their intentions for the world of humans. Thus the attempt to utilise these to make predictions in human affairs can be found in communities ranging from those of ancient Babylonia through even to Modern societies. Evidence of astrological considerations can be found in ancient Egyptian, Greek and Roman temples. Corresponding beliefs and practices in magic, religion, philosophy, mathematics, and astronomical observation can be found mixed together in a variety of forms. Numerous astrological works can be found written in Greek and Latin (generally incorporating earlier Egyptian and other astrological concepts). The earliest surviving systematic treatise was Manilius’s Astronomica written in Latin verse in the the first century (C1 AD).111 Early astrological instruments not surprisingly included variants of technologies used in other fields, from the counting board to the use of diagrams, inscriptions and calculations on papyrus, clay, stone and cloth. Using these, horoscopes and other astrological information could be developed and communicated. In particular, astrologers developed boards on which different configurations of the planets and stars could be illustrated by means of “pebbles” or more stylised counters. These counters could be moved to show the relationships of planets to the signs of the zodiac, to each other, and to the horizon. A surviving example is shown below.112

Ancient Greek astrological board - made of ivory, discovered at Grand (Vosges) C2 AD. From the outside, the concentric rings show names of ancient Greek astrological divisions (Decans), corresponding figures, terms expressed in Greek numerals, the Zodiac, and busts of Helios and Selene.
By the time of the first century AD increasingly methodical observations of the sun, moon, known planets, and background stars had been undertaken. It was with this heritage that Claudius Ptolemy (90 AD - 168 AD) set about writing his magisterial work on astronomy. It achieved in that field similar standing to that achieved by Euklid in his Elements in relation to geometry. Ptolemy was a Roman citizen, writing in Greek, and living and working in Alexandria, which was by then the capital city of the Roman province of Egypt. By now he had at his disposal not only the full power of Greek mathematics now at its zenith, but also Arisotle’s philosophically constructed picture of the earth. This had the Earth as the stationary centre of a cosmos around which the stars and planets moved in circles. Ptolemy also had available a history of recorded Greek astronomical observation (probably all of which works were available through the Library of Alexandria) - including specific references to Meton of Athens ( C5 BC), Callipus of Cyzicus (C4 BC), Aristarchus of Samos (C4–3 BC), Eratosthenes of Cyrene (C3–2 BC), and most notably Hipparchus of Nicaea (162–127 BC).
Titled variously as what transliterates as Mathematike Syntaxis in Greek, Syntaxis Mathematica in Latin, or The Almagest (the “Greatest”) by arab translators (which became the English title) and then printed in England (in Latin) as Almagestum (in 1515 AD)113, the book shows how with the Earth, as a stationary frame of reference, it is possible to build a model of the motion of the solar system as seen from the Earth. In this the Sun moves daily in a circle around the Earth, and each planet moves in a combination of two circles. The major circle (the deferent) is slightly offset from the Earth (by half the distance from a point for each planet known as the Equant), and the center of the other minor circle (the epicycle) moves around the circumference of the major circle. The model was remarkably accurate in relation to the observed motions of the planets. It provided a clear explanation of why the planets have apparently “wandering” paths in relation to the fixed stars. Ptolemy discovered that offsetting the centres of the deferents by the use of the Equant gave a greatly improved correspondence between theory and observation.114 So good was the result that Ptolemy’s model was to serve for some 1400 years until displaced, after a long ideological struggle by the heliocentric theory of Nicolaus Copernicus (1473–1543),115.
The Almagest was thus the most authoratitive exposition of astronomy to be produced in the pre-modern period. In it, as well as laying out the theory of the motions of the celestial bodies, Ptolemy lists the key measuring devices used to observe them. For example, he refers to the gnomon (a vertical stick from which the shadow of the sun as it moves can be measured) and armillary spheres (an astronomical device showing the concentric rings representing the major circles of the celestial sphere),116 and a mural quadrant (a graduated quarter circle inscribed on a wall, by means of which the elevation of celestial bodies could be measured).117
 |  |
| Representation of Ptolemy with | Ptolemeic armillary sphere |
| quadrant and armillary sphere118 | carried by Satyr119 |
| 1564 AD | 1575 |
A more refined device, the astrolabe, which combined the use of a quadrant with a form of mapping the stars through stereographic projection of their paths onto a plane, is attributed by some to Hipparchus (162–127 BC) who formalised the method of projection which was later utilised in the evolving device.
Perhaps the earliest description of an astrolabe like device appears once more in Vitruvius’s De architectura (~88–26 AD) where he describes an anaphoric clock.120 This device consisted of a large vertical disc rotated by a water wheel or other mechanism so that it turned through a complete revolution from sunrise of one day to the sunrise of the next. On the disk are marked the stars (or constellations of stars) of the Northern Hemisphere (together with those south of the equator down to the tropic of Capricorn - whose projection forms the outer limit of the disk). A circle represents the Zodiac - the path taken by the Sun in its journey across the sky over the year. Along the Zodiac circle are 365 holes, one for each day. On each successive day a marker for the Sun is to be advanced one hole to take account of the changing lengths of the day with season. In front of this rotating disk is a fixed disk of wires. A vertical wire marks the meridian (which divides the Earth from East to West). Concentric circles mark out selected months. Radial curved wires represent the 24 hours of the day as the Sun on its disk rotates behind them. Made for a particular location, a further curved wire arc lays out the horizon (below which stars on the disc still rotate, but cannot be seen at that place). This device, see below, thus displays the positions of selected groups of stars in the sky as they appear to move from a fixed point on Earth with the passing hours.121
 |  |
Left: a schematic representation of the wire grid pattern placed in front of anaphoric clock disk. Concentric circles mark lattitudes, radial curves mark the hours, wide arc marks the horizon122 Right: is from a modern representation (from an “ipad app”) of an “astrolabe clock”123 for a location on Earth 38 degrees North and 75 degrees West on 12 February 2012 at 9.22 PM. Sun, moon and planets can be seen on the Zodiac (red circle). Below the horizon is shaded gray. Green arrow through the sun shows the time on the 24 hour clock on the perimeter. In this modern representation the blue grid marks the angles of objects in vertical (altitude) and horizontal (azimuth) planes.124
The astrolabe itself is based on a similar idea but instead of the clock has a scale from which time can be read if the projected paths of the stars and hour is aligned to match the observed position of a selected star or stars. It was described by the Greek and mathematician scholar Theon of Alexandria (335–405 AD). (Theon was the father of daughter Hypatia (350–415 AD), whose unpleasant death at the hands of a Christian mob effectively ended the age of mathematical development in Alexandria.125) Theon’s description later would become a frequent reference for rediscovery of the device in later eras.
Immediately below is shown a modern representation of an anaphoric clock constructed by Prof . Kostas Kotsanas and his students. Next to it is an illustration from the 1886 Hoffmann’s catalogue for the sale of one of two fragments of such clocks discovered in the 19th century, in this case at Grand (Vosges) France. The sun marker is shown set at the second hour on the seasonally varying hour lines. Finally to the right is a photo of the front of an early astrolabe made by Jean Fusoris of Giraumont in the Ardennes region of France (1365–1415) and now held in the Adler Astronomy Planetarium and Museum in Chicago.
 |  |  |
| Representation of an anaphoric clock | Anaphoric fragment ~C2 AD | Early Astrolabe ~1400 AD |
| Recent replica126 | Catalogue illustration 1886127 | by Fusoris 1365–1414128 |
As the above suggests, the confluence of Greek geometric developments, philosophic inclinations, and systematic observation (albeit with the aid of what to Modern eyes appear comparatively simple instruments) was able to give rise to a mathematical description of the cosmos that was to serve for more than a millenium. The armillary was a simple static representation of some of these basic ideas. The anaphoric clock and astrolabe used more sophisticated geometric ideas to provide a more practically useable representation of the changing movements of constellations but with careful settings having to be made for day and either time or position of stars. However, extraordinarily, it appears that contemporaneously with this work, a mechanical mechanism had been devised which could model movements of the stars through time in a much more fluid and autonomous way enabling important and highly valued astronomical predictions to be made. This device, the most elaborate known to have existed in antiquity (and the most reminiscent of a Modern mechanical calculator or clock), is the Antikythera mechanism.
The Antikythera mechanism
A heavily corroded and encrusted set of 82 remnant fragments was discovered by Greek sponge divers in 1901. The fragments lay embedded amongst a range of treasures from C2-C1 BC in the wreck of an ancient Roman galleon at a depth of 60 metres off Point Glyphadia on the Greek island Antikythera. Whilst there has been more than a century of speculation on its mechanism and meaning the fragments have now yielded much greater detail to modern imaging technology. This reveals a highly complex ancient Greek mechanism complete with inscriptions which have been translated. In 2008 the mechanism was identified in an article in Nature as consisting of a device with a bronze system of interlocking cogs, and front and back output dials. The device, originally housed in a wooden frame, had some 30 intermeshed cogs which represented calendar cycles.129 The accuracy with which the mechanism was constructed is considered greater than any later known devices until clockwork mechanisms developed in the Middle Ages a thousand years later.130
 | ||
| Antikythera mechanism fragments ~150–80 BC | ||
 |  | |
| Antikythera main fragment | Antikythera dial fragment | |
| close up | close up | 131 |
By turning the wheels on this device with a handle the user was able to determine the relative positions of Sun and Moon. The lower back dial predicted luna eclipses whilst the upper dial was a Metonic calendar (based on the 19 year cycle the Moon takes, seen from a particular place on Earth, to return to the same place in the sky)132. All 12 months of the calendar have now been identified in relation to the device.
The Antikythera was of Corinthian origin, suggesting a heritage going back to Archimedes (who died in 212 BC). In support of this contention in 1974 Derek J De Solla Price pointed out that Cicero (106–43 BC) wrote that Archimedes built a planetarium which showed the Moon rise following the Sun above the Earth, together with eclipses and the motions of the five known planets, suggesting that the Antikythera had a similar purpose. However, the extent to which the Planetarium could have performed these claimed tasks has been open to controversy.133
The purposes of the Antikythera in any case should not be considered solely astronomical. An upper minor dial follows the four-year cycle of the Olympiad - the most important of the associated Panhellenic games. Thus the device, identified as being from about 100 BC, was “not simply an instrument of abstract science, but exhibited astronomical phenomena in relation to Greek social institutions.”134
A chasm exists in sophistication between this high-precision geared calculating device and the pebble accounting described earlier. Whilst much is unknown about it it is clear that the development and production of the Antikythera machine would have required high mathematical understanding, and the most sophisticated artisanal skills available. It is likely it was produced for a person or institution of the highest standing in Greek society who was able to call upon the most advanced talents of the day. The extraordinary accomplishments embodied in it tells us much about what could be achieved in the sophisticated society of ancient Greece in the later part of the “Golden Era” of Greek mathematical invention. But as well, this illustrates the dangers of assuming a sharp division between pragmatic and abstract mathematical cultures, or useful versus theoretical outcomes. This accomplishment clearly drew on high skills in both areas. Above all it is a reminder of the difference between perceived social need, and innovation - where invention actually finds use in practice. After all, where pebble accounting will do, why use anything more complicated and expensive?
This relationship between perceived need and innovation is strikingly illustrated by the fact that the principle of the steam engine was demonstrated in ancient Greece, in the form of the aeolipile (or “Hero’s engine”), more than two thousand years before the industrial revolution. As described by Hero of Alexandria, a hollow ball was caused to spin by steam blown out through two counterposed jets (for a diagram and explanation click here).135 It may well have been possible with the known technology at the time to extend this method to create a working steam powered machine. But it is likely there would have been little incentive to explore this possibility since there was plenty of slave labour available to the free citizens of the ancient Greek world. Indeed in the same tract in which the steam device is described there is serious attention paid to the perceived value of applying practical applications of pneumatic devices to producing mysterious effects for use in religious ceremonies.136
As the above suggests, apparently obvious developments may be ignored where no need for them is perceived. However, where power, authority or ceremony is seen to require a state of the art development, and sufficient resources are made available, then the best minds and most skilled talent may be brought to the task. It is not unreasonable to speculate that as with the success of the Manhattan and Moon Landing projects of the Twentieth Century (CE), some two thousand years before there were some of high authority also able to martial the best talents available. They too could create an object of technological achievement that would be a source of wonder for all privileged to view it. But whether it was through that means or the work of a School led by a Master who brought together the high artisanal, mathematical and empirical knowledge required, what is known is that for the time an extraordinarily refined analogue mechanical calculating device was made two millennia ago. The surviving evidence of that lies in the eroded but still comprehensible remains of the Antikythera mechanism.
3.5 Building on multiple pasts - the “Arabic hegemony”
As already noted, with the fall of the Western Roman empire around 500 AD, mathematical development from the ancient world had ceased.137 From the death of the prophet Mohammed at Medina in 632 AD there was a rapid expansion of the Islamic state which by 641 AD had included in its conquest much of Mesopotania and the former center of mathematical learning at Alexandria. The conquerers had little interest in mathematics. To the extent that they enjoyed collective unity it was primarily through economic exchange and shared tenets of the Islamic religion.
The following century was characterised by internal warfare and political turmoil. That began to subside around 750 AD. Following that there commenced a re-discovery of lost mathematical and scientific knowledge. Informally a process of diffusion of Indian, Greek and Persian knowledge had begun during the preceding century.138 A more formal and systematic process now began focussed on Baghdad under the three powerful patrons of learning - the caliphs al-Mansur (754–75 AD), Haroun al-Raschid (763–809 AD) and al-Mamun (812–33 AD). There al-Mamun, also regarded as the “glorious initiator” of the “translation movement”, established a “House of Wisdom” not unlike the prior Library of Alexandria.139 Once more the detail of what was rediscovered and further developments from that is described in detail elsewhere.140 It is sufficient to note here that Baghdad became a cosmopolitan centre of learning. But following Baghdad, over time the Arab world - comprising as it did a wide range of communities with diverse histories, backgrounds and cultures (including the Egyptian and Greek peoples) including also not only Muslims, but also Jews and Christians - provided a fertile background against which the desire to recapture and build on lost knowledge could be realised.
This civilisation took what it deemed necessary from the prior received knowledge. In relation to numerals the Indian system of discrete Hindu numerals, ordered in their places according to powers of ten, and with the zero included, slowly gained precedence. By the 16th Century it was giving rise to the Modern European system of “Indian-Arabic” numerals described earlier.141 Over the period from the eighth to the 15th centuries arabic mathematics developed to include:
- arithmetic primarily derived from India (including the principle of position);
- geometry rediscovered from ancient Greece but extended with a few additional general observations;
- trigonometry primarily from ancient Greece, but to which Hindu form, and additional functions and formulas were added, and with the most innovation; and
- algebra derived from Greek, Hindu and Mesopotanian sources but assuming a new and systematic form142 albeit still not expressed in the economical symbolic form that would later be created by Descartes, in the Modern era. (The term “algebra” derives from a book titled Kitab al-Jabr wal-Muqabala, published in the early ninth century by the famous mathematician and member of al-Mamun’s scientific academy, al-Khwarizmi, a page of which is shown below. It is the oldest known Arabic work on algebra.143)

Page from the Compendious Book on Calculation by Completion and Balancing (Kitab al-Jabr wal-Muqabala) by al-Khwarizmi: ~780–850 AD
The last of a line of great Muslim mathematicians of this period (who died in 1436), Al-Kashi, amongst his various achievements, calculated pi to 14 decimal places (in both sexagesimal and decimal forms), a notable feat not matched again until the late sixteenth century after the re-emergence of mathematical development in Europe.144
As to the technologies of calculation, the Islamic world had access to the counting boards, dustboards (used particularly in India), and abacus of the other civilisations that they had incorporated. One Damascus mathematician, al-Uqlidisi is known to have adapted the Indian system for pen and paper. Amongst the many advantages of this were the permanent recording and transmission of calculations using the efficient Indian notation.145 By this means the sharing of problems, equations, and methods for solving them was greatly facilitated and the basis for rapid development in a systematic form of mathematics, and particularly algebra (the word itself being derived from the Arabic), was established.
As already mentioned the measurement and prediction of the movement of celestial bodies has been central to many aspects of ancient life. These range across their astrological and religious implications, the timing of ceremonies, and the prediction of seasonal changes for agricultural purposes. This was no less true of the Islamic world where celestial observation was required to time the call to prayer, to determine the direction of Mecca, and to inform the work of astrologers. From the program supported by al-Mamun the Ptolmaic view of the universe became adopted everywhere in the Islamic world. The instruments named in the Almagest such as the gnomon, sun dial and quadrant, and armillary sphere were constructed and utilised. It was the C10 bilibliographer Ibn al Nadim who reported that al-Fazari was the first Muslim to have made an astrolabe.146 The astrolabe diffused through the Islamic world. Many of the most elegant were crafted under the direction of leading scholars who appeared, often with globes, in illustrations. These instruments could be found in many of the royal libraries as well as in the observatories which were constructed to systematise observations of the skies.
Of course the documentation of the history of mathematics and science is biased inevitably towards those areas that would have been recorded. Access to this would have been highly restricted, and was most likely to be found in Courts and Mosques. Certainly royal patronage was crucial in the early stages of reconstruction of ancient knowledge and in supporting the development of instruments and facilities of astronomical observation. This led to a pattern reminiscent of the “two cultures” already referred to. As noted earlier a division between “two cultures” of theoretical and pragmatic mathematics could be seen in the Athenian state of the Classical period. For the free citizenry forming the elite of this period (well serviced as they were by slaves and other non-citizens) the artisan or other person who performed work was thereby subordinated to the user of the products of that labour. Thus for Aristotle and Plato the free man is a user, never a producer. Ideally he uses things correctly but never transforms them by work.147 This explains in part the highly abstract presentation of mathematics by the Classical Greek mathematicians.
Similarly, the mathematics or science that was developed, or the instruments prepared for Court astronomy in the Arabic world, frequently had little of what might normally be considered practical application. Whether amongst the free elite in the slave society of ancient Greece, or the royal courts of the Arabic world, the actual doing of constructive work was something which the elite distanced themselves from and left to others. So the motivations for technical progress tended to either be the hope of attracting royal patronage, or ultimately not merely to satisfy a desire to advance knowledge but by being seen to do so to confirm the glory and wisdom of royalty who supported it. Having said that, much of great abstract value was accomplished through these means. Major developments included the construction of large observatories (one with a mural quadrant twenty metres in diameter) and the provision of employment to the most expert instrument makers.148
Further, as Charette points out, in a particularly valuable article, this discussion of usefulness tends to ignore another important use. That was the usefulness of science and scientific instruments for religious practice (as well as more mundane activities). Several leading astronomers (including the legendary al-Khwarizmi and Bayt al-Hikma) applied astronomical tables to the determination of prayer times and for predicting the religiously important first sighting of the lunar crescent. They laid out methods for finding the direction of Mecca, the construction of water clocks, sundials and hororaries, and the designs for sine quadrants and instruments for predicting lunar eclipses.149
Charette notes that from the middle of the C10, the progressive disintegration of the Abbasid empire led to a proliferation of local dynasties and principalities. This provided greater opportunity, in a diversity of places, in which patronage for astronomical and mathematical development might be found. Other centres such as Cairo and Damascus were also centers of such work over C13-C16. Whilst over this time the emphasis of patronage of such work in Courts diminished, the practical usefulness of the work in religious observance was picked up. As a consequence there was a diffusion (and to some extent rediscovery) of mathematical and astronomical knowledge and instrument making from Courts to Mosques. The boundary between Mosque and Public was in any case indistinct. These prized instruments, constructed in private shops, could been purchased by citizen and Mosque alike.150 By C15, the knowledge and possession of astronomical instruments such as the astrolabe, and the practical utility of it for determining time and direction, had become diffused more generally through Islamic society. However, the Islamic world was now shrinking under military pressure from Western Europe. It was being forced out of Spain, and the Renaissance was under way in the rising powers of Europe. This Renaissance was now dominated by the religion of Christianity, but nevertheless drew heavily on the Islamic world’s trove of rediscovered ancient knowledge together with the Islamic world’s own discoveries in mathematical and scientific knowledge, and invention of calculational and observational instruments.151
3.6 Dimensions of development
Enough has been said in what is inevitably a panoramic rather than detailed survey to suggest some (interconnected) factors that have shaped the direction and extent of development of different calculating technologies. These include the:
- value a society places on innovation and the existing stock of knowledge. The above history reflects an apparent rise and decline of social commitment to innovation together with the loss and rediscovery of past insights and developments. This can occur for different groups in society or for societies as a whole. The “Dark Ages” in Europe following the collapse of the Western Roman Empire (C5-C15) is an example of a time when mathematical innovation apparently lost much of its lustre and prior technical knowledge was, for a time, lost.
- complexity of social organisation and in particular the scale of hierarchical organisation and power and consequent organisation needs. With the extensive engineering works in ancient Mesopotania, and its more complex agricultural society, there was a need for more systematic means of calculation and development of approaches to meeting that need.
- relationship between perceptions of what needs to be done, and available or realisable technologies of calculation. This relationship goes both ways. The invention of new calculational approaches (for example of more efficient numeral systems, or of a system of geometry) also opens the possibility of new social needs emerging.
- dynamic interaction between mathematics and calculational technology. Developments in each of these depends on the developments in the other. As illustrated by the case of Roman numerals, even the form of numerals developed to write down quantities in part is shaped by the medium in which they are to be inscribed (for example, stone or parchment), the needs of the society to use them, and the technologies (such as pebbles or abacus) available to assist in manipulating them.
- relationship with users. From the Classical Greek period on we see the division emerging between the roles of calculation in the Courts, or the elites, which can lead to a distancing of developments from practical application needs, and the needs and capacities in the broader community. Instruments which are part of the play for patronage, or part of the process of celebrating power and standing may take a very different form, and play a very different role to those used as part of every day social interchange.
- relationship with producers of calculating technologies and their social position. Where artisans are required to develop such instruments they may play a very different social role to the users. The classical Greek divergence between theoretical mathematics and pragmatic artisanal mathematics has been referred to. Artisans not only have a social role, but also an accumulated knowledge that may be in part be encapsulated in embodied skills, and may routinely be transferred in non-codified forms. In various periods of history the guild-apprenticeship model has been the method of development of transference of this knowledge, the bulk or all of this being handed on through a mixture of oral instruction, and learned skills. Developments in this process may be directed much more sharply to solving perceived practical problems and may lead to quite different emphases and outcomes from those in more abstract and theoretical environments.
- extent of communication with other societies. Trade and other forms of communication with other societies enlarges the access to new knowledge, skills, and technological developments. The diffusion of Islamic knowledge (for example, about astronomy) to Europe and India, as well as Indian knowledge (and in particular the Islamic numeric script) to the Islamic world, provide examples of this.
- role of authority and power. The driving force of systems of authority, from the Egyptian pharonic society to the Islamic Caliphates, to the replacement of the Inca system of double accounting via the Khipu by the Spanish conquerers with European approaches,152 the role of authority and, as already mentioned, patronage, in shaping calculational approaches and technologies, is evident.
- breadth of need and literacy. Where the need for calculation is confined to a small subsection of society (for example, to priests of the dominant religion) then the need may be able to be met by training in traditional methods. But where the need spreads (for example, with trade and intensifying markets) then calculational technologies may offset the need for intense training in numerical and mathematical literacy. On the other hand, there is no need for technologies of calculation where there is no capacity to manipulate numbers. Thus the modes of education, whom they served and the breadth of their reach, and finally the extent of their numerical and mathematical content, will determine the usefulness, development, manufacture, and use of particular calculation instruments and approaches.
- role of specialisation. Specialised approaches such as those described earlier to measure and calculate astronomical or astrological phenomena may drive a particular direction of development which has little more general application, even though it may have very profound implications for some key processes. For example, the developments leading to the astrolabe was certainly of great importance for religious life and ultimately also for the organisation of social time and support of navigation and trade had great implications for society. But whilst associated developments in mathematics may have had many spin-offs, they were of a different character to those which directly seek to advance the overall power of mathematical calculation in a general way.
- cost and accessibility of calculational technology. Finally the utility of a calculating technology will be determined in part by its cost and accessibility. This will be determined by the extent that the problems it can solve are seen to be widely experienced, the training and literacy required to use it, and its cost of production. The use of instruments like the astrolabe or Roman abacus, let alone the Antikythera, were clearly circumscribed by what was required to construct them, in contrast, for example, to the use of pebbles for reckoning.
Consideration of the development of technologies of calculation in the Pre-Modern period suggests that these factors are helpful in understanding why particular technologies were developed and used at different times. As will be seen in Part 2 (next), they are also very useful in understanding what has shaped the directions of development in the dynamic Modern period which followed.
« Introduction | | Part 2 The Modern Era »
1 see for example, papers cited in http://www.scientificamerican.com/article.cfm?id=how-animals-have-the-ability-to-count, Michael Tennesen, “More Animals Seem to Have Some Ability to Count”, Scientific American, September 2009, viewed 19 Dec 2011. (↑)
2 Nicholas Carr, The Shallows: What the Internet is Doing to Our Brains, W. W. Norton, New York and London, 2010 (↑)
3 Brian D. Ripley, Pattern recognition and neural networks, Cambridge University Press, UK, 1996 (↑)
4 Tennesen, Scientific American, op. cit. (↑)
5 Ivilin Stoianov and Marco Zorzi, “Emergence of a ‘visual number sense’ in hierarchical generative models”, Nature Neuroscience, advance online publication, Sunday, 8 January 2012/online, http://dx.doi.org/10.1038/nn.2996 (viewed 21 Jan 2012) (↑)
6 Celeste Biever, “Neural network gets an idea of number without counting”, New Scientist, Issue 2848, 20 Jan 2012. (↑)
7 Jonathan Grainger, Stéphane Dufau, Marie Montant, Johannes C. Ziegler, Joël Fagot, “Orthographic Processing in Baboons (Papio papio)”, Science, Vol. 336 no. 6078, 13 April 2012, pp. 245–248. (↑)
8 J.M. Adovasio, O. Soffer, D.C. Hyland Textiles and cordage, Pavlov I – Southeast: A window into the Gravettian lifestyles, Dol. Vest. Stud. 14, Brno, 2005, p. 432–443, cited in http://paleo.revues.org/index607.html by Jiri A. Svoboda , “The Gravettian on the Middle Danube” Paléo [En ligne] , 19, 2007 , mis en ligne le 23 avril 2009, Consulté le 21 décembre 2011 (↑)
9 Stephen Chrisomalis, “The cognitive and cultural foundations of numbers”, Oxford Handbook, pp. 495–502. (↑)
10 Carl B. Boyer and Uta C. Merzbach, History of Mathematics, Wiley, 2010, p. 2. (↑)
11 ibid p. 7. (↑)
12 Jonas Bogoshi, Kevin Naidoo, John Webb, The Oldest Mathematical Artefact, The Mathematical Gazette, Vol. 71, No. 458 (Dec., 1987), p. 294. (↑)
13 D. Huylebrouck, “The Bone that Began the Space Odyssey”, The Mathematical Intelligencer, Vol. 18, No. 4, pp. 56–60 (↑)
14 Frank J. Swetz, “Bodily Mathematics” in From Five Fingers to Infinity: A Journey through the History of Mathematics, Open Court, Chicago, 1994, p. 52. (↑)
15 John Harris, “Australian Aboriginal and Islander mathematics”, Australian Aboriginal Studies, number 2, 1987, pp. 29–37. (↑)
16 Denise Schmandt-Besserat, “The Origins of Writing: An Archaeologist’s Perspective”, Written Communication, Vol 3, 1986, p. 35. (↑)
17 See, for example, http://khipukamayuq.fas.harvard.edu (↑)
18 Gary Urton, “Mathematics and Authority: a case study in Old and New World Accounting”, in Robson and Stedall, The Oxford handbook, p. 34–49. (↑)
19 From the Museum for World Culture, Göteborg, Sweden. Image retained in the Harvard University Khipu Database at khipukamayuq.fas.harvard.edu/images/KhipuGallery/MiscAlbum/images/UR113%20Valhalla_jpg.jpg (viewed 27 Dec 2011) (↑)
20 Denise Schmandt-Besserat, “The Origins of Writing : An Archaeologist’s Perspective”, Written Communication Vol 3, No1, January, 1986, Figure 3, p. 41. For more of the work of this eminent author see Denise Schmandt-Besserat (ed.), Symbols at ‘Ain Ghazal, in Ghazal Excavation Reports 3, bibliotheca neolithica Asiae meridionalis et occidentals, 2013, & Yarmouk University, Monograph of the Faculty of Archaeology and Anthropology, 2013; Denise Schmandt-Besserat , Before Writing: From writing to cuneiform, The University of Texas Press, USA, 1992, and Denise Schmandt-Besserat, How Writing came about, University of Texas Press, USA, 1996. (↑)
21 Denise Schmandt-Besserat, “The Envelopes That Bear the First Writing”, Technology and Culture, Vol. 21, No. 3, July 1980, Figure 1, p. 358. (↑)
22 see for example, Zimansky, “Review of Schmandt-Besserat 1992”, in Journal of Field Archaeology, Vol. 20, 1993, pp. 513–7. (↑)
23 Schmandt-Besserat, Written Communication, 1986, p. 37. (↑)
24 for example, Livio C. Stecchini, “The Origin of the Alphabet”, American Behavioral Scientist, Vol 4, February, 1961, pp. 3–7 (↑)
25 See, for example, http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Babylonian_numerals.html (↑)
26 Translation thanks to Bob Englund, private communication, 18 March 2014, who stresses that it needs further interpretation by an expert in Old Babylonian administrative script. (↑)
27 Eleanor Robson, “Mathematical Education in an Old Babylonian Scribal School”, in Robson and Stedall, The Oxford handbook, Figure 3.1.4, p. 210. (↑)
28 Friberg notes that in the transliteration of this text in A Remarkable Collection, 69, there is a mistake in the last line. Instead of 54 26 15, read 44 26 40. Jöran Friberg, private communication, 22 August 2013. (↑)
29 ibid (↑)
30 Eleanor Robson, “Mathematics education in an Old Babylonian scribal school”, in Robson and Stedall, The Oxford handbook, pp. 209–227 (↑)
31 Chrisomalis, Oxford Handbook, p. 509. (↑)
32 Stephen Chrisomalis, “A Cognitive Typology for Numerical Notation”, Cambridge Archaeological Journal Vol 14, Issue 1, 2004, p. 37. (↑)
33 ibid, p. 51. (↑)
34 characters reproduced from Boyer and Merzbach, History of Mathematics, p. 10 (↑)
35 For a more detailed account of the multiple scripts which emerged and a classification of them see Georges Ifrah, The Universal History of Computing: From the Abacus to the Quantum Computer, John Wiley & Sons, USA, 2001, pp. 26–63. (↑)
36 except where otherwise indicated script images reproduced from http://en.wikipedia.org/wiki/List_of_numeral_systems (viewed 23 Dec 2011) (↑)
37 Chrisomalis, Cambridge Archaeological Journal, 2004, pp. 51–2. (↑)
38 image created with MS Word (↑)
39 script images reproduced in modified form from David Kerkhoff, “Hieratic Numerals” http://www.dafont.com/hieratic-numerals.font (viewed 24 Dec 2011 (↑)
40 script images reproduced in modified form from Jan Meyer, “Die Entwicklung der Zahlensysteme” http://www.rechenhilfsmittel.de/zahlen.htm (viewed 17 Jan 2012) (↑)
41 script images reproduced in modified form from Jan Meyer, ibid. (↑)
42 script images reproduced in modified form from Jan Meyer, ibid. (↑)
43 An accurate rendition of Modern numerals appears on the title page of Juan de Yciar, Libro Intitulado Arithmetica Practica, Zaragoza, 1549 (↑)
44 There is much debate in the literature about whether the Egyptians used this property in the construction of the Pyramids. In sum there is probably no evidence that they did, but some evidence they may have used it in the construction of tombs. The only firm evidence that this relationship was known and taught is from a Demotic papyrus from the third century BC. There is earlier suggestive evidence. See Corinna Rossi, Architecture and Mathematics in Ancient Egypt, Cambridge University Press, Cambridge, UK,2004, p. 9. (↑)
45 Measuring the land using rope, from the Tomb Chapel of Menna, New Kingdom, Valley of the Nobles, Thebes, Egypt, contained in the Bridgeman Art Library, reproduced at various sites on the web including civilization.ca/civil/egypt/images/fback3b.jpg (viewed 26 Dec 2011) and with fuller description at gettyimages.com.au/detail/illustration/measuring-the-land-using-rope-from-the-tomb-chapel-of-stock-graphic/55995332 (↑)
46 Loa-tze, Tao-teh-king, English Edition, P. Carus (ed.), Chicago, 1898, pp. 137, 272, 323, cited in David Eugene Smith and Yoshio Mikami, A History of Japanese Mathematics, The Open Court Publishing Company, Chicago, 1914, p. 20 (↑)
47 at kaleidoscope.cultural-china.com/en/137K6K6434.html|Cultural China (viewed 28 Dec 2011) (↑)
48 Smith and Mikami, A History of Japanese Mathematics, p. 20. (↑)
49 From Mayake Kenryu’s work of 1795, reproduced in Smith and Mikami, A History of Japanese Mathematics, p. 29. (↑)
50 ibd, p. 21 (↑)
51 see for example, http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Babylonian_mathematics.html, “An overview of Babylonian mathematics”, viewed 21 December 2011 (↑)
52 For some nice images of the various types of abacus which emerged from different cultures see http://en.wikipedia.org/wiki/Abacus, the coresponding Wikpedia article (viewed 23 Dec 2011) (↑)
53 ibid (↑)
54 Boyer and Merzbach, History of Mathematics, pp. 179–80. (↑)
55 see Karl Menninger, A Cultural History of Numbers, Dover, 1992 (republication of MIT Press English Translation, 1969, of the German Edition, Zahlwot und Ziffer: Eine Kulturgeschichte der Zahlen, Vanderhoek & Ruprecht, Germany, 1957–1958); and more generally http://en.wikipedia.org/wiki/Roman_abacus - the corresponding Wikpedia article. (viewed 23 Dec 2011) (↑)
56 The oldest surviving counting board, made of marble. Photo from the National Museum of Epigraphy, Athens, reproduced from Menninger, A Cultural History of Numbers, Fig. 128, p. 300. (↑)
57 Image below and is adapted from a photography by Mark Cartwright (http://www.ancient.eu.com/image/2147/) of the object held at the Museo Archeologico Reionale of the Regione autonomy Valle d’Aosta, Greece, where it was discovered in a tomb along with other grave goods. As has noted by Searfimo Cuomo (see http://www.gresham.ac.uk/lectures-and-events/early-mathematics-day), since grave goods were both indicators of status and also were connected to, or possessions of the deceased, it raises the possibility that this was the grave of a professional ‘calculator’. An image of another such abacus from the Museo Nazionale Ramano at Piazzi delle Terme, Rome - can be found reproduced at http://www.ee.ryerson.ca/~elf/abacus/roman-hand-abacus.html. Made of brass plate it is approximately 115 x 99 mm with nine long slots (equipped with four sliders for 1–4) and eight short slots each with one slider (for 5). The eight left most columns run in powers of ten from units on the right to millions on the left. The ninth slot is for a fraction of ounces. Further details can be found in Cesare Rossi, Flavio Russo and Ferrucio Russo, “Ancient Engineers and Inventions, History of Mechanism and Machine Science, Springer, Vol. 8, 2009, p. 42. Other embodiments consisted of a grooved counting board, or simply a table on which counters could be moved. (see Karl Menninger, A Cultural History of Numbers, Dover, 1992 (republication of MIT Press English Translation, 1969, of the German Edition, Zahlwot und Ziffer: Eine Kulturgeschichte der Zahlen, Vanderhoek & Ruprecht, Germany, 1957–1958); and more generally http://en.wikipedia.org/wiki/Roman_abacus - the corresponding Wikpedia article. (viewed 23 Dec 2011) (↑)
58 James Cusick, “The Japanese Soroban: A Brief History and Comments on its Role”, http://www.jamescusick.net/pages/hosdocs/Cusick_SorobanHistory.pdf (viewed 11 June 2011) (↑)
59 see for example, http://sites.google.com/site/osakasoroban/news/soroban|Osaka Abacus Association, “Soroban: The first calculator” (viewed 23 Dec 20110. (↑)
60 “regulae quae a sudantibus abacistis vix intelleguntur” - “rules which the sweating abacists scarcely understand”, quoted in Menninger, A Cultural History of Numbers, p. 327 (↑)
61 Menninger, A Cultural History of Numbers, p. 298 et seq. (↑)
62 See http://www.ee.ryerson.ca/~elf/abacus/abacus-contest.html, “The Abacus vs. the Electric Calculator” (viewed 28 Dec 2011). (↑)
63 See also http://www.britishpathe.com/record.php?id=44628|see also newsreel footage of a similar competition in Hong Kong in 1967 (viewed 28 Dec 2011). (↑)
64 Smith and Mikami, A History of Japanese Mathematics, p. 19; and a similar argument from Boyer and Merzbach, History of Mathematics, p. 228 (↑)
65 G.E.R Lloyd “What was mathematics in the ancient world?”, in Robson and Stedall, The Oxford handbook, p. 8. (↑)
66 Corinna Rossi, “MIxing, building and feeding: mathematics and technology in ancient Egypt”, in Robson and Stedall, The Oxford handbook, p. 418 (↑)
67 British Museum, “Rhind Mathematical Papyrus” http://www.britishmuseum.org/explore/highlights/highlight_objects/aes/r/rhind_mathematical_papyrus.aspx (viewed 1 Jan 2012) (↑)
68 Rossi in Robson and Stedall, The Oxford handbook, pp. 407–8. (↑)
69 source at 3.bp.blogspot.com/_Om5WdRNbuEE/RhR7fCaoGfI/AAAAAAAAABs/4K8uUPqpLPc/s320/rhind.jpg (viewed 30 Dec 2011) (↑)
70 see for example, http://en.wikipedia.org/wiki/COBOL (↑)
71 see for example, Marshall Clagett, Ancient Egyptian Science: A Source Book, Volume Three, “Ancient Egyptian Mathematics”, American Philosophical Society, Philadelphia, 1999. (↑)
72 For more on this see for example, Annette Imhausen, “Ancient Egyptian Mathematics: New Perspectives on Old Sources”, The Mathematical Intelligencer, Vol. 28, No. 1, 2006, pp. 19–27. (↑)
73 Boyer and Merzbach, History of Mathematics, p. 19. (↑)
74 Ibid., p 20. (↑)
75 see for example, Rossi, “Mixing, Building and Feeding”, Oxford Handbook, pp. 407–428. (↑)
76 Boyer and Merzbach A History of Mathematics, pp. 21–2. (↑)
77 Ibid p. 25 (↑)
78 From Boyer and Merzbach A History of Mathematics, p. 34. (↑)
79 Ibid pp. 26–39 (↑)
80 Jöran Friberg, private communication, 23 August 2013. (↑)
81 Boyer and Merzbach A History of Mathematics, pp. 195–7. (↑)
82 ibid p. 196 (↑)
83 ibid p. 198–203 (↑)
84 ibid p. 204 (↑)
85 ibid pp. 206–11. (↑)
86 ibid p. 211–3 (↑)
87 see for example http://en.wikipedia.org/wiki/History_of_mathematics (viewed 14 Jan 2012) and references contained therein. (↑)
88 Carl B. Boyer and Uta C. Merzbach, History of Mathematics, Wiley, 2010, pp. 43–52. (↑)
89 Boyer and Merzbach, History of Mathematics, pp. 176–191 (↑)
90 ibid, p. 192 (↑)
91 Marcus Asper, “The two cultures of mathematics in ancient Greece”, “, in Robson and Stedall, The Oxford handbook, p.107. (↑)
92 ibid (↑)
93 ibid pp.108–114 (↑)
94 Lloyd “What was mathematics in the ancient world?”, The Oxford handbook, pp. 9–10. (↑)
95 Greek citizens chosen each year in ancient Athens to sit in judgement on issues brought before them (↑)
96 http://classics.mit.edu/Aristophanes/wasps.htmlThe Wasps by Aristophanes, English translation provided by The Internet Classics Archive (viewed 19 Jan 2012). (↑)
97 ibid, pp. 9–18 (↑)
98 Asper, “The two cultures of mathematics in ancient Greece”, p. 124. (↑)
99 ibid, pp. 128–9. (↑)
100 ibid (↑)
101 ibid pp. 108–9 (↑)
102 ibid p. 109. (↑)
103 Boyer and Merzbach, History of Mathematics, pp. 191–192 (↑)
104 Boyer and Merzbach, History of Mathematics, p. 177 (↑)
105 Hammurabi’s Code of Laws, tr. L. W. King, http://www.sacred-texts.com/ane/ham/ham04.htm, viewed 23 March 2014. (↑)
106 Menninger, A Cultural History of Numbers, Fig 183, p. 306. (↑)
107 cf. Latin noun: calculator - arithmetician or accountant; verb: calculo, calculare, calculavi, calculatus sum - reckon or calculate (↑)
108 This argument is made in extensive detail in http://worlds-in-transition.com by Joseph Camilleri and Jim Falk, Worlds in Transition: Evolving Governance Across a Stressed Planet, Edward Elgar, London, UK, 2009. (↑)
109 For a description of the Roman understanding of the celestial movements, the implications for the hours in a day, and the construction of sundials and water clocks to measure the passage of time in relation to these movements, see Marcus Vitruvius Pollo (~ 80 BC–15 BC), de architectura, translated by Morris Hicky Morgan as The Ten Books of Architecture, Book IX, http://en.wikisource.org/wiki/Ten_Books_on_Architecture/Book_IX (viewed 25 Jan 2012). (↑)
110 For a subtle discussion of the role and design of Stonehenge see for example Lionel Sims, “The 'Solarization' of the Moon: Manipulated Knowledge at Stonehenge”, Cambridge Archaeological Journal, vol 16, 2006, pp. 191–207 (↑)
111 James E Evans, “The Astrologer's Apparatus: A Picture of Professional Practice in Greco-Roman Egypt”, Journal for the History of Astronomy, Vol 35, Part 1, No 118, February 2004, pp. 1–44. (↑)
112 ibid, Fig 1., p. 6. (↑)
113 Claudius Ptolemaeus, Almagestum: Opus ingens ac nobile omnes Celorum motus continens. Felicibus Astris eat in lucem, 1515. Copy in the Institut für Astronomie, Universität Wien, Türkenschanzstraße 17, 1180 Wien reproduced at http://www.univie.ac.at/hwastro/books/1515_ptole_BWLow.pdf (viewed 31 Jan 2012) (↑)
114 Richard Fitzpatrick, A Modern Almagest: An Updated Version of Ptolemy’s Model of the Solar System, University of Texas at Austin, http://farside.ph.utexas.edu/syntaxis/Almagest.pdf, (viewed 27 Jan 2012), p. 6. (↑)
115 Nicolaus Copernicus, De revolutionibus orbium coelestium, Holy Roman Empire of the German Nation, Nuremberg, 1543 (↑)
116 Ptolemy, Almagest, Book 1 section 6 or . For a translation see http://www.brycecorkins.com/wp-content/uploads/documents/PtolemysAlmagest.pdf (viewed 28 Jan 2012) (↑)
117 William Cecil Dampier, A history of science and its relations with philosophy & religion, University Press, Cambridge, 1929, p. 49. (↑)
118 annon, Ptolemy from Clavdio Tolomeo Principe De Gli Astrologi, et De Geografi, Giordano Ziletti, Venezia, 1564 http://www.er.uqam.ca/nobel/r14310/Ptolemy/Ziletti.html (viewed 28 Jan 2012) (↑)
119 museo galileo Institute and Museum of the History of Science, VII.36 Model of the solar orb http://brunelleschi.imss.fi.it/museum/esim.asp?c=407036 (viewed 28 Jan 2012) (↑)
120 Vitruvius, De architectura, Book VIII, “Sundials and Water Clocks”, sections 8–15^ http://www.mlahanas.de/Greeks/Texts/Vitruvius/Book9.html (viewed 29 Jan 2012) (↑)
121 A. G. Drachmann, “The Plane Astrolabe and the Anaphoric Clock”, Centaurus, vol 3, issue 1, 1970, pp. 184–9 (↑)
122 Drachmann, “The Plane Astrolobe”, Fig. 1, p. 184. (↑)
123 For a nice description of the progressive development of the astrolabe clock see George Burnett-Stuart, “Astronomical Clocks of the Middle Ages: A Guided Tour”, http://www.almagest.co.uk/middle/astclk.htm (viewed 2 Feb 2012) (↑)
124 http://itunes.apple.com/au/app/astrolabe-clock/id421777015?mt=8 (viewed 1 Feb 2012) (↑)
125 Boyer and Merzbach, History of Mathematics, p. 192 (↑)
126 Portion of a replica constructed by Prof . Kostas Kotsanas and his students; extracted from a photo by Augusta Stylianou, http://www.mlahanas.de/Greeks/Technology/AncientGreekTechnology001.html (viewed 29 Jan 2012) (↑)
127 Illustration from 1886 Hoffmann sale catalogue showing Grand (Vosges) fragment of anasphoric clock now in the museum in Saint-Germain-en-Laye. Shown in John North, God’s Clockmaker: Richard of Wallingford and the Invention of Time, Continuum, Londong, 2006 (first published 2005), p. 152. (↑)
128 Front of Fusoris astrolabe (Photo from the Adler Planetarium and Astronomy Museum, reproduced at http://astrolabes.org/pages/fusoris.htm (viewed 29 Jan 2012) (↑)
129 Philip Ball, “Complex clock combines calendars”, Nature, vol 454, published online 30 July 2008, p. 561, http://www.nature.com.ezp.lib.unimelb.edu.au/news/2008/080730/full/ (viewed 14 October 2011) (↑)
130 T. Freeth, Y. Bitsakis, X. Moussas, J.H. Seiradakis, A.Tselikas, E. Magkou, M. Zafeiropoulou, R. Hadland, D. Bate, A. Ramsey, M. Allen, A. Crawley, P. Hockley, T. Malzbender, D. Gelb, W. Ambrisco and M.G. Edmunds, “Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism”, Nature vol 444, 2006, pp. 587–591 (↑)
131 Original images Rien van de Weygaert, Sept. 2002, National Archaeological Museum Athens, http://www.astro.rug.nl/~weygaert/antikytheraoriginal.html (viewed 24 Jan 2012 (↑)
132 See for example, http://www.astrocal.co.uk/metonic-cycle.htm (viewed 25 Jan 2012) (↑)
133 See, for example, “Archimede’s Planetarium”, Museo Galilleo, http://brunelleschi.imss.fi.it/vitrum/evtr.asp?c=8253 (viewed 25 Jan 2012). (↑)
134 Tony Freeth, Alexander Jones, John M. Steele and Yanis Bitsakis, “Calendars with Olympiad display and eclipse prediction on the Antikythera Mechanism”, Nature, vol 456, 31 July 2008, pp. 614–617. (↑)
135 The Pneumatics of Hero of Alexandria, Translated for and Edited by Bennet Woodcraft, Taylor Walton and Maberly, London, 1851. Reproduced at http://www.history.rochester.edu/steam/hero/section50.html (viewed 25 Jan 2012) (↑)
136 see index, ibid, http://www.history.rochester.edu/steam/hero/index.html (viewed 25 Jan 2012) (↑)
137 Except where otherwise noted, all of the detail in this section (including the helpfully descriptive phrase “Arabic hegemony” is drawn from the excellent treatment in Boyer and Merzbach A History of Mathematics, Chapter 13, pp. 225–45. (↑)
138 François Charette, “The Locales of Islamic Astronomical Instrumentation”, History of Science, xliv, 2006, p. 124 (↑)
139 ibid, p. 124 (↑)
140 Boyer and Merzbach A History of Mathematics, pp. 225–45. (↑)
141 ibid p. 237 (↑)
142 ibid p. 240 (↑)
143 John L. Esposito (ed), The Oxford History of Islam, Oxford University Press, UK, 1999, p 186. (↑)
144 ibid pp. 244–5 (↑)
145 http://www.islamicspain.tv/Arts-and-Science/The-Culture-of-Al-Andalus/Mathematics.htm (↑)
146 Ibn al-Nadim (ed. by R. Tajaddud), Ktab al-Fihrist, Tehran, 1971, p. 332 (cited in Charette, Locales, p.124). (↑)
147 Herbert A. Applebaum, The Concept of Work: Ancient, Medieval and Modern, State University of New York Press, Albany, 1992, p. 31 (↑)
148 Charette, “The Locales”, p. 125. (↑)
149 ibid, p. 126. (↑)
150 ibid. pp. 128–132 (↑)
151 Alison Abbott, “Islamic Science: Rebuilding the Past”, Nature, Vol 432, 16 Dec 2004, pp. 795–5. (↑)
152 See Robsan and Stedall, The Oxford Handbook, Chapter 1.2, pp. 27–55. (↑)
« Introduction | | Part 2 The Modern Era »
Pages linked to this page
 This work by Jim Falk is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License Click on the logo to the left to see the terms on which you can use it.
This work by Jim Falk is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License Click on the logo to the left to see the terms on which you can use it.